6.7. Ôn tập chương VI
Hướng dẫn giải bài tập SGK toán lớp 8 tập 1 trang 132, 133. Bài học Ôn tập chương VI.
Nội dung chính
Bài 41. (Trang 132 SGK Toán 8 – Tập 1)
Cho hình chữ nhật 
. Gọi 
lần lượt là các trung điểm của 
Tính:
a) Diện tích tam giác 
b) Diện tích tứ giác 
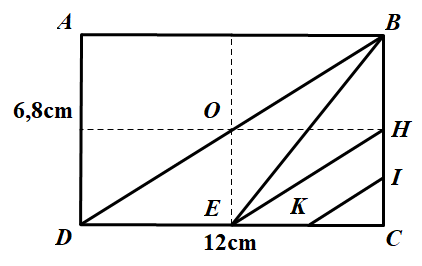
Bài giải:
a) Diện tích tam giác
Ta có: 
* Tam giác DBC vuông ở C có hai cạnh góc vuông là:
Do đó 
Do đó 
Vậy 
b) Diện tích tứ giác EHIK:
Ta có 
* 
* 
Vậy 
Bài 42. (Trang 132 SGK Toán 8 – Tập 1)
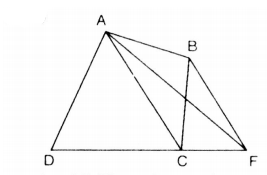
Hình vẽ trên có AC // BF, hãy tìm tam giác có diện tích bằng diện tích của tứ giác ABCD.
Bài giải:
Ta có thể bài toán cụ thể như sau: Cho tứ giác ABCD vẽ đường chéo AC. Từ B vẽ BF // AC (F nằm trên đường thẳng DC). Nối AF.
Ta tìm được tam giác ADF có diện tích bằng diện tích tứ giác ABCD.
* Chứng minh: Thật vậy, vì AC // BF nên khoảng cách từ B và F đến AC là bằng nhau. Hơn nữa hai tam giác ABC và AFC có cùng cạnh AC. Do đó 
. Ta có: 
Vậy ta tìm được tam giác ADF có diện tích bằng diện tích tứ giác ABCD (đpcm)
Bài 43. (Trang 133 SGK Toán 8 – Tập 1)
Cho hình vuông ABCD có tâm đối xứng O, cạnh a. Một góc vuông xOy có tia Ox cắt cạnh AB tại E, tia Oy cắt cạnh BC tại F (hình dưới). Tính diện tích tứ giác OEBF.
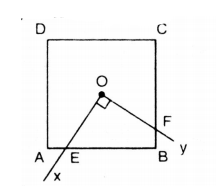
Bài giải:
Vẽ hai đường chéo AC và BD của hình vuông ABCD cắt nhau tại O. Chúng chia hình vuông ABCD ra bốn tam giác vuông bằng nhau, suy ra diện tích 4 tam giác đó cũng bằng nhau.
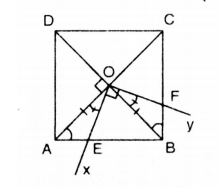
Vậy 
– Xét hai tam giác AOE và tam giác BOF, ta có:
OA = OB (tính chất đường chéo hình vuông)
và 
Vậy 
– Ta có: 
(cộng 2 vế của (2) với 
)
hay 
– Từ (1) và (3) ta có: 
Bài 44. (Trang 133 SGK Toán 8 – Tập 1)
Gọi O là điểm nằm trong hình bình hành ABCD. Chứng minh rằng tổng diện tích của hai tam giác ABO và DCO bằng tổng diện tích của hai tam giác BCO và DAO.
Bài giải:
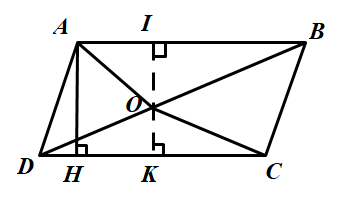
Qua O vẽ IK vuông góc với AB và DC (
)
Ta có:
Ta có: 
Từ (1) và (2) ta có:
(đpcm)
Bài 45. (Trang 133 SGK Toán 8 – Tập 1)
Hai cạnh của một hình bình hành có độ dài là 6cm và 4cm. Một trong các đường cao có độ dài là 5cm. Tính độ dài đường cao kia.
Bài giải:
Gọi đường cao còn lại là h.
Theo quan hệ giữa đường xiên và hình chiếu thì ta có chiều cao của hình bình hành luôn nhỏ hơn cạnh không tương ứng với nó.
⇒ Đường cao có độ dài bằng 5cm ứng với cạnh 4cm
⇒ SABCD = 4.5 = 20
Mà SABCD = h.6
⇒ h.6 = 20 ⇒ h = 20 : 6 = 3,33 (cm).
Bài 46. (Trang 133 SGK Toán 8 – Tập 1)
Cho tam giác ABC. Gọi M, N là các trung điểm tương ứng của AC, BC. Chứng minh rằng diện tích hình thang ABNM bằng diện tích của tam giác ABC.
Bài giải:
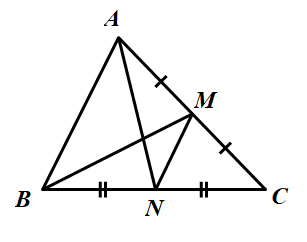
Vẽ hai trung tuyến AN và BM của tam giác ABC. Ta có:
(vì đó là đáy bằng nhau và cùng chiều cao)
(vì đó là đáy bằng nhau và cùng chiều cao)
Cộng (1) và (2) vế theo vế, ta có:
hay 
Vậy 
Bài 47. (Trang 133 SGK Toán 8 – Tập 1)
Vẽ ba đường trung tuyến của một tam giác (hình dưới). Chứng minh sau tam giác: 1, 2, 3, 4, 5, 6 có diện tích bằng nhau.
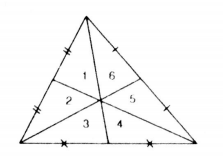
Bài giải:
Theo hình vẽ ta gọi tên sáu tam giác là: 1, 2, 3, 4, 5 và 6.
Vì đường trung tuyến của tam giác chia cạnh đáy ra làm hai phần bằng nhau nên ta có:
(vì có đáy bằng nhau và cùng chiều cao) (1)
(vì có đáy bằng nhau và cùng chiều cao) (2)
(vì có đáy bằng nhau và cùng chiều cao) (3)
Ta còn có: 
(vì chúng bằng 
) (4)
Thay (1), (2), (3) vào (4) ta suy ra: 
Ta cũng có: 
Thay (1), (2), (3) vào (6) ta suy ra được: 
Kết hợp (1), (2), (3), (6), (7) ta suy ra được:
Xem thêm: Hướng dẫn giải bài tập sách giáo khoa Định lí Ta-lét trong tam giác.
Bạn có thể in hoặc xuất file pdf! Thật tuyệt!
