8.8. Diện tích xung quanh của hình chóp đều
Hướng dẫn giải bài tập SGK toán lớp 8 tập 2 trang 121. Bài học Diện tích xung quanh của hình chóp đều
Nội dung chính
Bài 40. (Trang 121 SGK Toán 8 – Tập 2)
Một hình chóp tứ giác đều có độ dài cạnh bên bằng 25cm, đáy là hình vuông ABCD cạnh 30cm. TÍnh diện tích toàn phần của hình chóp.
Bài giải:
Vẽ
Vậy SH là trung đoạn của hình chóp. Đặt SH = d. Vì S.ABCD là hình chóp tứ giác đều nên tam giác SBC là tam giác cân và đường cao SH cũng là đường trung tuyến.
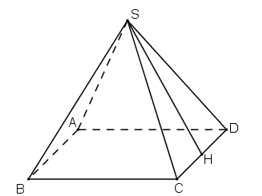

Do đó:
Áp dụng định lí Pitago trong tam giác vuông HSB, ta có:
Nửa chu vi đáy của hình chóp là:
Vậy diện tích xung quanh hình chóp là:
Diện tích đáy hình chóp là:
Vậy diện tích toàn phần hình chóp S.ABCD là:
Vậy
Bài 41. (Trang 121 SGK Toán 8 – Tập 2)
Vẽ, cắt và gấp miếng bìa như đã chỉ ra ở hình vẽ bên dưới để được hình chóp tứ giác đều.
a) Trong hình a), có bao nhiêu tam giác cân bằng nhau?
b) Sử dụng định lí Pitago để tính chiều cao ứng với đáy của mỗi tam giác.
c) Diện tích xung quanh và diện tích toàn phần của hình chóp đều này là bao nhiêu?
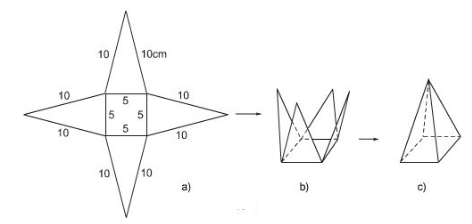

Bài giải:
a) Vì hình vẽ trên là chóp tứ giác đều đáy là hình vuông. Do đó 4 mặt bên là những tam giác cân bằng nhau (c-c-c)
b) Vẽ
Áp dụng định lí Pitago trong tam giác vuông SHB, ta có:
Vậy
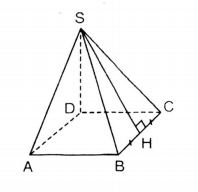

c) * Diện tích xung quanh của hình chóp:
– Nửa chu vi đáy của hình chóp là:
– Diện tích xung quanh của hình chóp là:
* Diện tích toàn phần của hình chóp là:
Ta có:
Vậy diện tích toàn phần hình chóp là:
Bài 42. (Trang 121 SGK Toán 8 – Tập 2)
Tính độ dài đường cao của hình chóp tứ giác đều với các kích thước cho trên bài 41.
Bài giải:
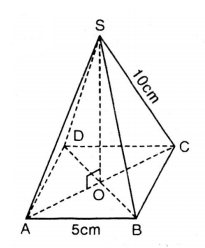

Gọi O là giao điểm của hai đường chéo hình vuông ABCD. Khi đó O là tâm đường tròn đi qua 4 đỉnh hình vuông ABCD.
Nối SO, khi đó SO là đường cao hình chóp S.ABCD hay
Vì ABCD là hình vuông có cạnh AB = 5cm.
Do đó
Áp dụng định lí Pitago trong tam giác vuông SAO, ta có:
Vậy
Bài 43. (Trang 121 SGK Toán 8 – Tập 2)
Tính diện tích xung quanh, diện tích toàn phần của các hình chóp tứ giác đều sau đây (hình dưới)
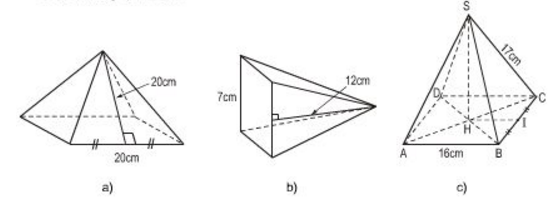

Bài giải:
a) Hình a): Vì S.ABCD là hình chóp tứ giác đều nên ABCD là hình vuông.
Do đó nửa chu vi đáy là:
Vì SBC là tam giác cân nên đường cao SH cũng là trung đoạn của hình chóp đều. Vậy diện tích xung quanh hình chóp đều S.ABCD là:
Diện tích đáy là:
Vậy diện tích toàn phần là:
b) Hình b): Tính tương tự câu a) ta có kết quả:
c) Hình c): Lí luận tương tự bài bài tập mẫu, ta có:
– Chiều cao mặt bên hình chóp là:
– Diện tích xung quanh hình chóp là:
– Diện tích đáy hình chóp là:
Vậy diện tích toàn phần hình chóp là:
Xem thêm Hướng dẫn giải bài tập sách giáo khoa Thể tích của hình chóp đều.

