5.3. Hình thang cân

Hướng dẫn giải bài tập sgk toán lớp 8 tập 1 trang 74-75. Bài học:  Hình thang cân

Bài 11. (Trang 74 SGK Toán 8 – Tập 1)

Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (h.30, độ dài của cạnh ô vuông là 1cm)

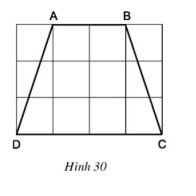
Bài giải:

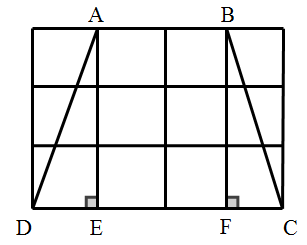
Vì độ dài của cạnh ô vuông là 1cm nên độ dài của cạnh:

Áp dụng định lí Py ta go trong tam giác vuông EAD, ta có:

Vì tứ giác ABCD là hình thang cân nên :

Vậy độ dài các cạnh của hình thang ABCD là:

Bài 12. (Trang 74 SGK Toán 8 – Tập 1)

Cho hình thang cân ABCD  . Kẻ các đường cao AE, BF của hình thang. Chứng minh rằng .

Bài giải:

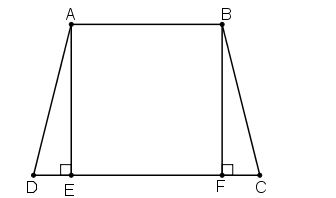
Vì ABCD là hình thang cân nên ta có:

Xét hai tam giác vuông EAD và FBC ta có:

Vậy (ch-gn). Suy ra (dpcm)

Bài 13. (Trang 74 SGK Toán 8 – Tập 1)

Cho hình thang cân ABCD , E là giao điểm của hai đường chéo. Chứng minh rằng .

Bài giải:

 

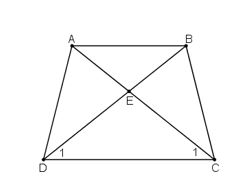
Do ABCD là hình thang cân nên:

Xét hai tam giác ADC và BCD, ta có:

DC: cạnh chung

(c.c.c) (hai góc tương ứng)

cân tại E

Mà hay

Vậy

Bài 14. (Trang 75 SGK Toán 8 – Tập 1)

Đố: Cho các tứ giác ABCD và EFGH trên giấy kẻ ô vuông (h.31), tứ giác nào là hình thang cân ?

Vì sao ?

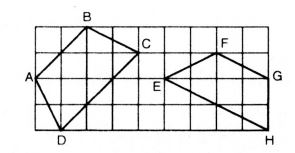
Bài giải:

Quan sát và nhận xét ta thấy:

Tứ giác ABCD là hình thang cân.

Tứ giác EFGH là hình thang như không là hình thang cân vì .

Bài 15. (Trang 75 SGK Toán 8 – Tập 1)

Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D và E sao cho .

a) Chứng minh rằng BDEC là hình thang cân.

b) Tính các góc của hình thang cân đó, biết rằng

Bài giải:

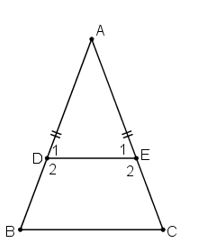
a) Ta có cân

có:

Mà nên

  (1)

có:

Mà (vì cân tại A)

  (2)

Từ (1) và (2) suy ra

Mà hai góc ở vị trí đồng vị 

Suy ra tứ giác DECB là hình thang.

Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.

b) , thay vào (2) ta được:

Lại có

Mà

DECB là hình thang cân

Vậy

Bài 16. (Trang 75 SGK Toán 8 – Tập 1)

Cho tam giác ABC cân tại A, các đường phân giác BD, CE . Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Bài giải:

cân tại A (giả thiết)

(tính chất tam giác cân)

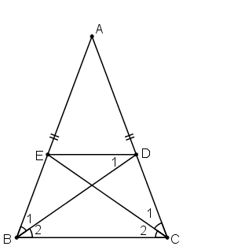
Vì BD, CE là lần lượt là phân giác của và (giả thiết)

   (tính chất tia phân giác)

Mà (chứng minh trên)

Xét và có:

(cmt)

chung

(g.c.g)

(2 cạnh tương ứng)

Ta có: (cmt) nên cân tại A

Xét có:

Xét có:

Mà (cmt)

Từ (1) và (2) , mà hai góc này ;à góc đồng vị nên suy ra DE // BC

Do đó BEDC là hình thang cân

Ta có: (so le trong)

Lại có nên

cân tại E

(tính chất tam giác cân)

Vậy BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Bài 17. (Trang 75 SGK Toán 8 – Tập 1)

Hình thang ABCD (AB // CD) có . Chứng minh rằng ABCD là hình thang cân.

Bài giải:

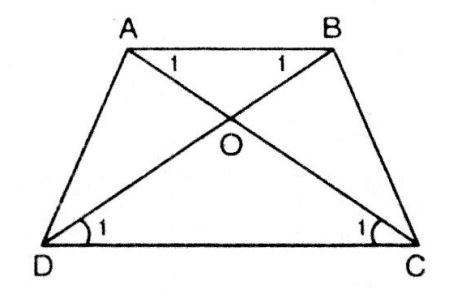
Gọi O là giao điểm của hai đường chéo AC và BD

Xét , ta có:

Vậy cân tại O      (1)

Vì AB // CD (gt); so le trong với suy ra

Vì AB // CD (gt); so le trong với suy ra

Mà

Vậy cân tại O. Suy ra    (2)

Từ (1) và (2) ta có:

Bài 18. (Trang 75 SGK Toán 8 – Tập 1)

Chứng minh định lý “Hình thang có hai đường chéo bằng nhau là hình thang cân” qua bài toán sau: Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E. Chứng minh rằng:

a) là tam giác cân

b)

c) Hình thang ABCD là hình thang cân.

Bài giải:

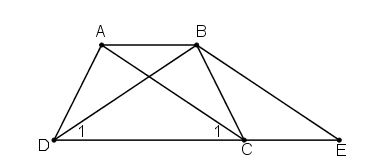
VÌ AB // DC (gt)

Do hai đoạn thẳng song song chắn bởi hai đường thẳng song song (AC // BE)

Mà AC = BD (gt)

Suy ra BD = BE

Xét , ta có: BD = BE

Vậy cân tại B (đpcm)

b) Vì cân tại B nên ta có:    (1)

Vì AC // BE (gt); và là hai góc đồng vị

Suy ra     (2)

Từ (1) và (2) suy ra :

Xét hai tam giác ACD và BDC có:

AC = BD (gt)

(cmt)

DC: cạnh chung

Vậy (đpcm)

c) Vì ABCD là hình thang (gt)

Và (vì )

Vậy ABCD là hình thang cân (đpcm)

Bài 19. (Trang 75 SGK Toán 8 – Tập 1)

Đố: Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32). Hãy tìm điểm thứ tư M là giao điểm của các dòng kẻ sao cho nó với ba điểm đã cho là bốn đỉnh của một hình thang cân.

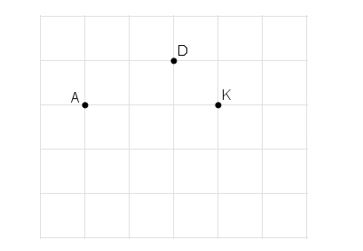
Bài giải:

Học sinh tự làm.

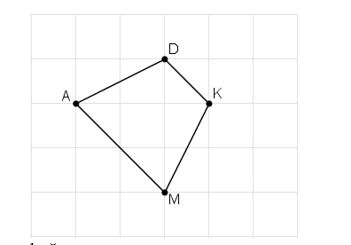
Điểm được xác định như hình vẽ bên. Em hãy trình bày cách xác định vị trí điểm M.

Xem thêm hướng dẫn giải bài tập sgk toán 8. Đường trung bình của tam giác, hình thang