8.7. Hình chóp đều và hình chóp cụt đều
Hướng dẫn giải bài tập SGK toán lớp 8 tập 2 trang 118, 119. Bài học Hình chóp đều và hình chóp cụt đều.
Nội dung chính
Bài 36. (Trang 118 SGK Toán 8 – Tập 2)
Quan sát hình bên dưới và điền cụm từ và số thích hợp vào các ô trống ở bảng sau, biết rằng các hình đã cho là những hình chóp đều.
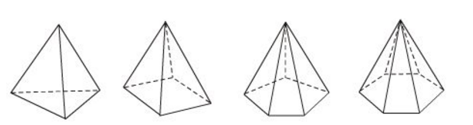
| Chóp tam giác đều | Chóp tứ giác đều | Chóp ngũ giác đều | Chóp lục giác đều | |
| Đáy | Tam giác đều | |||
| Mặt bên | Tam giác cân | |||
| Số cạnh đáy | 5 | |||
| Số cạnh | 10 | |||
| Số mặt | 5 |
Bài giải:
| Chóp tam giác đều | Chóp tứ giác đều | Chóp ngũ giác đều | Chóp lục giác đều | |
| Đáy | Tam giác đều | Hình vuông | Ngũ giác đều | Lục giác đều |
| Mặt bên | Tam giác cân | Tam giác cân | Tam giác cân | Tam giác cân |
| Số cạnh đáy | 3 | 4 | 5 | 6 |
| Số cạnh | 6 | 8 | 10 | 12 |
| Số mặt | 4 | 5 | 6 | 7 |
Bài 37. (Trang 118 SGK Toán 8 – Tập 2)
Xét sự đúng, sai của phát biểu sau:
a) Hình chóp đều có đáy là hình thoi và chân đường cao trùng với giao điểm hai đường chéo của đáy.
b) Hình chóp đều có đáy là hình chữ nhật và chân đường cao trùng với giao điểm hai đường chéo của đáy.
Bài giải:
a) SAI vì hình chóp đều có đáy phải là đa giác đều mà hình thoi không phải là đa giác đều (hình vuông là tứ giác đều).
b) SAI vì hình chữ nhật không phải là hình đa giấc đều nên không có hình chóp đều đáy là hình chữ nhật.
Bài 38. (Trang 119 SGK Toán 8 – Tập 2)
Trong các tấm bìa ở hình bên dưới, em hãy gấp lại tấm bìa nào thì có được một hình chóp đều.
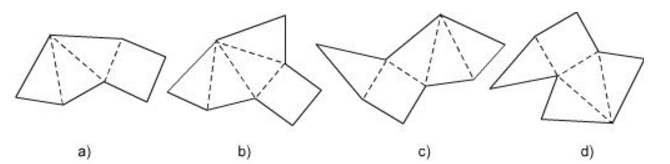
Bài giải:
– Hình a khi gấp lại thì không được một hình chóp đều vì đáy là tứ giác đều nhưng chỉ có ba mặt bên thay vì phải có 4 mặt bên.
– Hình b và hình c khi gấp lại thì được một hình chóp tứ giác đều.
– Hình d khi gấp lại thì không được một hình chóp tứ giác đều vì ở trên cùng một cạnh đáy có đến 2 mặt bên còn trên một cạnh đáy thì không có mặt bên nào.
Bài 39. (Trang 119 SGK Toán 8 – Tập 2)
Thực hành: Từ tờ giấy cắt ra một hình vuông rồi thực hiện các thao tác theo thứ tự từ 1 đến 6 đê có thể ghép được cấc mặt bên của hình chóp tứ giác đều (hình dưới)
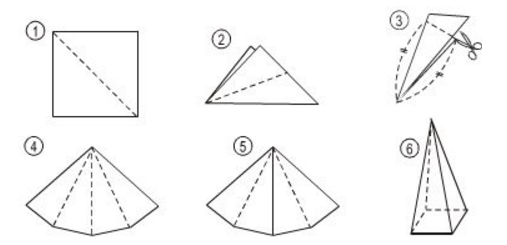
Bài giải:
Học sinh tự thực hành.
Xem thêm Hướng dẫn giải bài tập sách giáo khoa Diện tích xung quanh của hình chóp đều.

