5.9. Đường thẳng song song với một đường thẳng cho trước
Hướng dẫn giải bài tập sgk toán lớp 8 tập 1 trang 102-103. Bài học: Đường thẳng song song với một đường thẳng cho trước
Nội dung chính
Bài 67. (Trang 102 SGK Toán 8 – Tập 1)
Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C, D, E sao cho AC = CD = DE (h.97). Kẻ đoạn thẳng EB. Qua C, D kẻ các đường thẳng song song với EB. Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau.
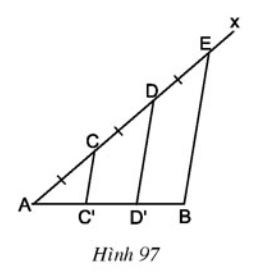
Bài giải:
Xét , ta có:
, CC’ đi qua trung điểm của cạnh AD’ của
Suy ra:
Vì . Vậy tứ giác CC’BE là hình thang
Ta còn có: và
Vậy DD’ đi qua trung điểm của cạnh C’B của hình thang CC’BE
Suy ra
Từ (1) và (2) ta có: (dpcm)
Bài 68. (Trang 102 SGK Toán 8 – Tập 1)
Cho điểm A nằm ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. Lấy điểm B bất kì thuộc đường thẳng d. Gọi C là điểm đối xứng với điểm A qua điểm B. Khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào ?
Bài giải:
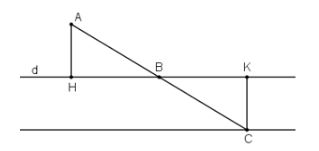
Gọi H, K là hình chiếu của A và C trên đường thẳng d
Khoảng cách từ A đến d bằng AH
Xét vuông tại H và
vuông tại K có:
AB = AC
(cạnh huyền- góc nhọn)
Vậy điểm C nằm trên đường thẳng song song với d, không đi qua A và cách d 2cm
Bài 69. (Trang 103 SGK Toán 8 – Tập 1)
Ghép mỗi ý (1), (2), (3), (4) với một trong các ý (5), (6), (7), (8) để được một khẳng định đúng :
| (1) Tập hợp các điểm cách điểm A cố định một khoảng 3cm | (5) là đường trung trực của đoạn thẳng AB |
| (2) Tập hợp các điểm đều hai đầu của đoạn thẳng AB cố định | (6) là hai đường thẳng song song với a và cách a một khoảng 3cm |
| (3) Tập hợp các điểm nằm trong góc xOy và cách đều hai cạnh của góc đó | (7) là đường tròn tâm A bán kính 3cm |
| (4) Tập hợp các điểm cách đều đường thẳng a cố định một khoảng 3cm | (8) là tia phân giác của góc xOy |
Bài giải:
Ta có:
(1) – (7)
(2) – (5)
(3) – (8)
(4) – (6)
Bài 70. (Trang 103 SGK Toán 8 – Tập 1)
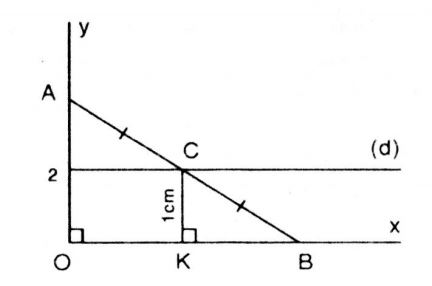
Cho góc vuông xOy, điểm A thuộc tia Oy sao cho . Lấy B là một điểm bất kì thuộc tia Ox. Gọi C là trung điểm của AB. Khi điểm B di chuyển trên tia Ox thì điểm C di chuyển trên đường nào ?
Bài giải:
Trong tam giác vuông OAB từ trung điểm C của cạnh AB ta kẻ
Khi đó
Vậy CK là đường trung bình của tam giác OAB. Suy ra
Vậy điểm C cách đường thẳng cố định Ox một khoảng không đổi bằng 1cm. Vậy khi điểm B di chuyển trên tia Ox thì điểm C di chuyển trên đường thẳng d song song với tia Ox và cách Ox một khoảng không đổi bằng 1cm.
Bài 71. (Trang 103 SGK Toán 8 – Tập 1)
Cho tam giác ABC vuông tại A. Lấy M là một điểm bất kì thuộc cạnh BC. Gọi MD là đường vuông góc kẻ từ M đến AB, ME là đường vuông góc kẻ từ M đến AC, O là trung điểm của DE.
a) Chứng minh rằng 3 điểm A, O, M thẳng hàng.
b) Khi điểm M di chuyển trên cạnh BC thì điểm O di chuyển trên đường nào ?
c) Điểm M ở vị trí nào trên cạnh BC thì AM có độ dài nhỏ nhất ?
Bài giải:
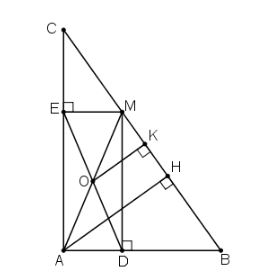
a) Ta có tứ giác ADME có:
Suy ra ADME là hình chữ nhật
O là trung điểm của đường chéo DE nên O cũng là trung điểm của đường chéo AM
Vậy A, O, M thẳng hàng.
b) Kẻ
Ta có: (cùng vuông góc BC)
OK là đường trung bình của tam giác MAH
Điểm O cách BC một khoảng cố định bằng
Suy ra O nằm trên đường thẳng song song với BC
Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB
Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC
c) Vì AH là đường cao hạ A đến BC nên (trong tam giác vuông thì cạnh huyền là cạnh lớn nhất).
Vậy AM nhỏ nhất khi M trùng H.
Xem thêm hướng dẫn giải bài tập sgk toán 8. Hình thoi

