6.4. Diện tích hình thang

Hướng dẫn giải bài tập SGK toán lớp 8 tập 1 trang 125, 126. Bài học Diện tích hình thang.

Bài 26. (Trang 125 SGK Toán 8 – Tập 1)

Tính diện tích mảnh đất hình thang ABED theo các độ dài đã cho trên hình và biết diện tích hình chữ nhật ABCD là

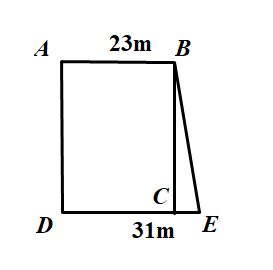
Bài giải:

Ta có:

Vậy diện tích hình thang ABED là:

Vậy .

Bài 27. (Trang 125 SGK Toán 8 – Tập 1)

Vì sao hình chữ nhật ABCD và hình bình hành ABEF lại có cùng diện tích? Hãy suy ra cách vẽ một hình chữ nhật có cùng diện tích với một hình bình hành cho trước.

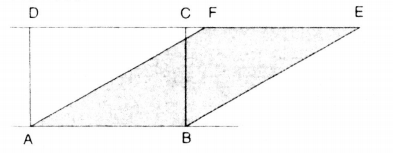
Bài giải:

– Vì hình chữ nhật ABCD và hình bình hành ABEF có đáy chung là AB và có chiều cao bằng nhau. Vậy diện tích của chúng bằng nhau.

– Cách vẽ hình chữ nhật có cùng diện tích với hình bình hành cho trước, ta vẽ như sau:

Trước hêt ta vẽ hình bình hành ABEF. Ta kéo dài cạnh  EF. Từ A và B ta vẽ hai đường thẳng cùng vuông góc với đường thẳng EF nối dài cắt nó lần lượt tại C và D, ta có hình chữ nhật ABCD là hình cần dựng.

Bài 28. (Trang 126 SGK Toán 8 – Tập 1)

Xem hình bên dưới (IG // FU). Hãy đọc tên một số hình có cùng diện tích với hình bình hành FIGE.

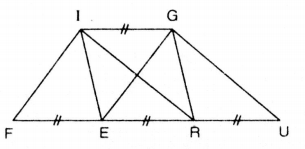
Bài giải:

Xét các hình bình hành FIGE, IGRE, IGUR và các tam giác IFR, GEU, ta có:

– Chiều cao các hình bình hành và các tam giác trên bằng nhau (do IG // FU)

– Đáy của tam giác gấp đôi đáy của các hình bình hành.

Dựa vào công thức tính diện tích hình bình hành và diện tích tam giác ta được:

.

Bài 29. (Trang 126 SGK Toán 8 – Tập 1)

Khi nối trung điểm của hai đáy hình thang, tại sao ta được hai hình thang có diện tích bằng nhau?

Bài giải:

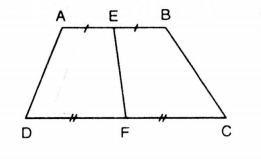
Xét hai hình thang: AEFD và BEFC ta có:

– Chúng cùng chiều cao.

– Có các đáy bằng nhau: AE = EB và DF = FC.

Vậy diện tích của chúng bằng nhau: .

Bài 30. (Trang 126 SGK Toán 8 – Tập 1)

Trên hình dưới ta có hình thang ABCD với đường trung bình EF và hình chữ nhật GHIK. Hãy so sánh diện tích hai hình này, từ đó suy ra một cách chứng minh khác về công thức diện tích hình thang.

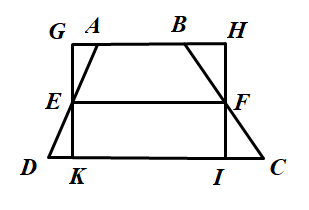
Bài giải:

Cho hình thang ABCD (AB // CD) ta dựng hình chữ nhật GHIK có một cạnh bằng đường trung bình của hinh thang và có diện tích bằng diện tích hình thang.

Ta dễ dàng chứng minh:

Suy ra

Mà nên

Ở đây ta gặp lại công thức tính diện tích hình thang đã học nhưng bằng một phương pháp khác, đó là:

Diện tích hình thang bằng tích đường trung bình với đường cao của nó.

Bài 31. (Trang 126 SGK Toán 8 – Tập 1)

Xem hình bên dưới, hãy chỉ ra các hình có cùng diện tích (lấy ô vuông làm đơn vị diện tích)

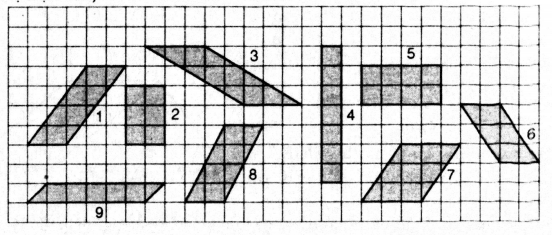
Bài giải:

Các hình 2, 6, 9 có cùng diện tích là 6 (ô vuông)

Các hình 1, 5, 8 có cùng diện tích là 8 (ô vuông)

Các hình 3, 7 có cùng diện tích là 9 (ô vuông)

Xem thêm: Hướng dẫn giải bài tập sách giáo khoa Diện tích hình thoi.