6.3. Diện tích tam giác

Hướng dẫn giải bài tập SGK toán lớp 8 tập 1 trang 121, 122, 123. Bài học Diện tích tam giác.

Bài 16. (Trang 121 SGK Toán 8 – Tập 1)

Giải thích vì sao diện tích của tam giác được tô đậm trong các hình a) b) c) chứng tỏ được diện tích của tam giác bằng nửa diện tích hình chữ nhật tương ứng:

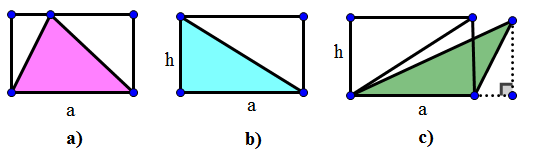
Bài giải:

Các cạnh của hình chữ nhật ở hình a), b), c) có chiều dài là a và chiều rộng là h. Vậy diện tích của các hình chữ nhật đó là:

Các tam giác ở các hình a), b), c) có cạnh đáy là a và chiều cao tương ứng là h. Vậy diện tích các tam giác đó là:

So sánh (1) và (2) ta có:

Điều này chứng tỏ rằng diện tích của tam giác bằng nửa diện tích của hình chữ nhật tương ứng.

Bài 17. (Trang 121 SGK Toán 8 – Tập 1)

Cho tam giác AOB vuông tại O với đường cao OM (hình bên).

Hãy giải thích vì sao ta có đẳng thức:

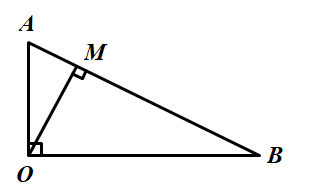
Bài giải:

Nếu lấy cạnh AB và đường cao tương ứng với nó là OM thì diện tích tam giác OAB là:

Vì tam giác OAB vuông tại O nên diện tích tam giác OAB là:

Từ (1) và (2) suy ra: (đpcm)

Bài 18. (Trang 121 SGK Toán 8 – Tập 1)

Cho tam giác ABC và đường trung tuyến AM. Chứng minh:

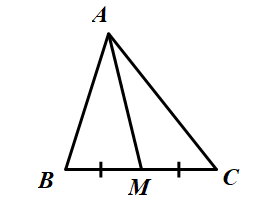
Bài giải:

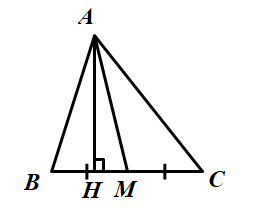
Vẽ đường cao AH ứng với cạnh BC của tam giác ABC. Vì AM là trung tuyến của tam giác ABC nên MC = MB.

Ta có:

và

Vậy (đpcm)

Bài 19. (Trang 122 SGK Toán 8 – Tập 1)

a) Xem hình dưới đây, hãy chỉ ra các tam giác có cùng diện tích (lấy ô vuông làm đơn vị diện tích)

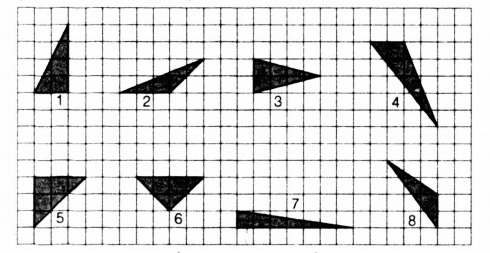
b) Hai tam giác có diện tích bằng nhau thì có bằng nhau hay không?

Bài giải:

a) Ta có:

Vậy tam giác ở hình 1, 3, 6 có cùng diện tích. Hình 2 và 8 có cùng diện tích

b) Nói chung thì hai tam giác có diện tích bằng nhau thì không bằng nhau.

Bài 20. (Trang 122 SGK Toán 8 – Tập 1)

Vẽ hình chữ nhật có một cạnh bằng một cạnh của một tam giác cho trước và có diện tích bằng diện tích của tam giác đó.

Từ đó suy ra một cách chứng minh khác về công thức tính diện tích tam giác.

Bài giải:

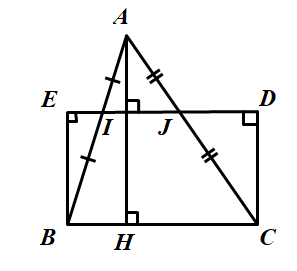
Ta dựng hình chữ nhật có một cạnh là cạnh của tam  giấc ABC, cạnh đối diện thuộc đường thẳng đi qu a trung điểm của hai cạnh còn lại.

Để chứng minh diện tích tam giác ABC bằng diện tích hình chữ nhật BCDE, ta kẻ

Ta có

và

Như vậy:

Kết quả này cho chúng ta một cách chứng minh công thức diện tích tam giác.

Bài 21. (Trang 122 SGK Toán 8 – Tập 1)

Tính sao cho diện tích hình chữ nhật ABCD gấp ba lần diện tích tam giác ADE.

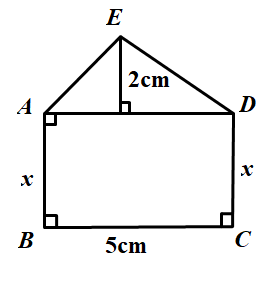
Bài giải:

Ta có:

và

Theo đề bài ta có:

hay

Vậy

Bài 22. (Trang 122 SGK Toán 8 – Tập 1)

Tam giác PAF được vẽ trên giấy kẻ ô vuông (hình vẽ)

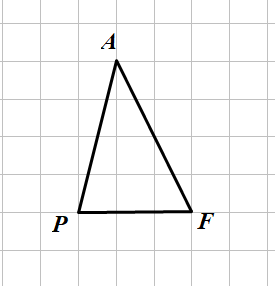
Hãy chỉ ra:

a) Một điểm I sao cho

b) Một điểm O sao cho

c) Một điểm  N sao cho

Bài giải:

a) Có vô số điểm I nằm trên đường thẳng đi qua A và song song với PF sẽ thỏa mãn điều kiện

b) Vì điểm A cách PF một khoảng bằng 4 đơn vị. Do đó điểm O thỏa mãn điều kiện: thì điểm O phải cách PF một khoảng bằng 8 đơn vị. Có vô số điểm như thế.

c) Vì điểm A cách PF một khoảng bằng 4 đơn vị. Do đó điểm N thỏa mãn điều kiện:  thì điểm N phải cách PF một khoảng bằng 2 đơn vị.

Bài 23. (Trang 123 SGK Toán 8 – Tập 1)

Cho tam giác ABC. Hãy chỉ ra một số vị trí của điểm M nằm trong tam giác đó sao cho:

.

Bài giải:

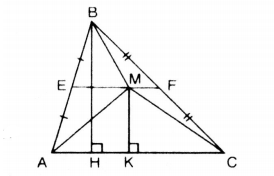
Theo giả thiết điểm M nằm trong tam giác ABC sao cho:

Ta có:

Vì tam giác MAC và tam giác ABC có chung đáy AC nên:

Vậy điểm M nằm trên đường trung bình EF của tam giác ABC.

Bài 24. (Trang 123 SGK Toán 8 – Tập 1)

Tính diện tích của một tam giác cân có đáy bằng a và cạnh bên bằng b.

Bài giải:

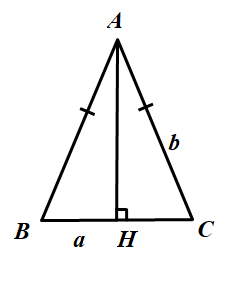
Giả sử tam giác ABC cân tại A.

Vẽ đường cao AH.

Khi đó AH cũng là đường trung tuyến và

Áp dụng định lí Py-ta-go trong tam giác vuông HAB, ta có:

Ta có diện tích tam giác cân ABC:

Bài 25. (Trang 123 SGK Toán 8 – Tập 1)

Tính diện tích của một tam giác đều có cạnh bằng a.

Bài giải:

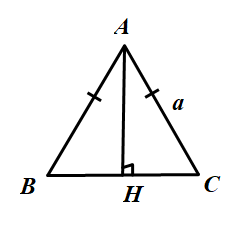
Vẽ đường cao AH, tương tự bài 24 ta tính được

Khi đó

Vậy

Xem thêm: Hướng dẫn giải bài tập sách giáo khoa Diện tích hình thang.