6.1. Sự xác định của đường tròn. Tính chất đối xứng của đường tròn
Hướng dẫn giải bài tập trong sách giáo khoa toán lớp 9 tập 1 trang 99, 101. Bài học: Sự xác định của đường tròn. Tính chất đối xứng của đường tròn
Nội dung chính
- Bài 1. (Trang 99 SGK Toán 9 – Tập 1)
- Bài 2. (Trang 100 SGK Toán 9 – Tập 1)
- Bài 3. (Trang 100 SGK Toán 9 – Tập 1)
- Bài 4. (Trang 100 SGK Toán 9 – Tập 1)
- Bài 5. (Trang 100 SGK Toán 9 – Tập 1)
- Bài 6. (Trang 100 SGK Toán 9 – Tập 1)
- Bài 7. (Trang 101 SGK Toán 9 – Tập 1)
- Bài 8. (Trang 101 SGK Toán 9 – Tập 1)
- Bài 9. (Trang 101 SGK Toán 9 – Tập 1)
Bài 1. (Trang 99 SGK Toán 9 – Tập 1)
Cho hình chữ nhật ABCD có . Chứng minh rằng bốn điểm A, B, C, D thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.
Bài giải
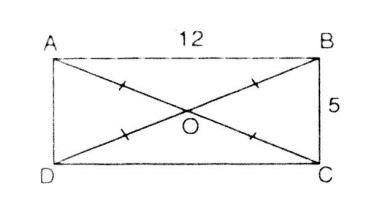
Gọi O là giao điểm của hai đường chéo AC và BD hình chữ nhật ABCD.
Suy ra:
Suy ra bốn điểm A, B, C, D cách đều điểm O nên bốn điểm này cùng thuộc đường tròn tâm O.
Xét tam giác ABC vuông tại B, áp dụng định lí Pitago, ta có:
Bán kính đường tròn là:
Bài 2. (Trang 100 SGK Toán 9 – Tập 1)
Hãy nối mỗi ô ở cột trái với mỗi ô ở cột phải để được khẳng định đúng :
| (1) Nếu tam giác có ba góc nhọn | (4) thì tâm của đường tròn ngoại tiếp tam giác đó nằm bên ngoài tam giác |
| (2) Nếu tam giác có góc vuông | (5) thì tâm của đường tròn ngoại tiếp tam giác đó nằm bên trong tam giác |
| (3) Nếu tam giác có góc tù | (6) thì tâm của đường tròn ngoại tiếp tam giác đó là trung điểm của cạnh lớn nhất |
| (7) thì tâm của đường tròn ngoại tiếp tam giác đó là trung điểm của cạnh nhỏ nhất |
Bài giải
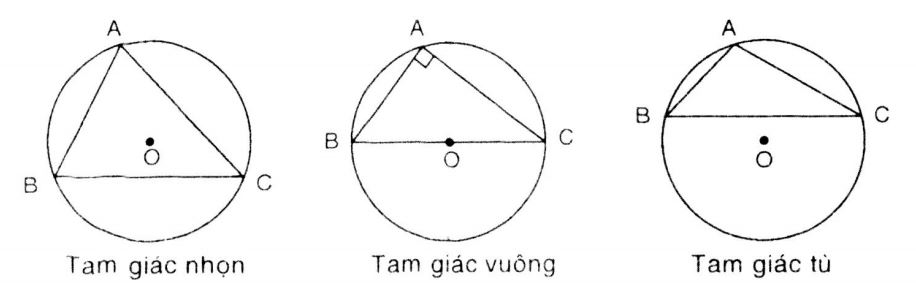
Như vậy: Nối (1) với (5); (2) với (6); (3) với (4)
Bài 3. (Trang 100 SGK Toán 9 – Tập 1)
Chứng minh các định lí sau:
a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
Bài giải
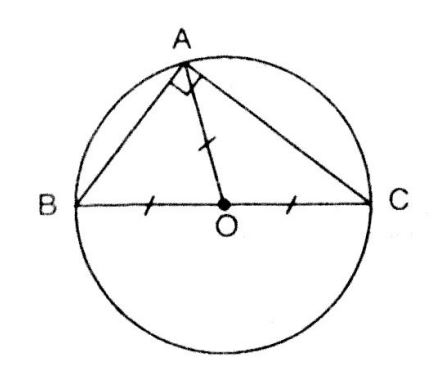
a) Trong tam giác vuông ABC, ta có AO là đường trung tuyến ứng với cạnh huyền BC nên:
Vậy trung điểm O của cạnh huyền là tâm của đường tròn ngoại tiếp tam giác vuông đó.
b) Xét nội tiếp trong đường tròn tâm O, đường kính BC.
Nối AO, khi đó AO là đường trung tuyến của
Suy ra:
Mà trong một tam giác đường trung tuyến ứng với một cạnh và bằng nửa cạnh đó là tam giác vuông
Vậy
Bài 4. (Trang 100 SGK Toán 9 – Tập 1)
Trên một mặt phẳng tọa độ Oxy, hãy xác định vị trí của mỗi điểm
Bài giải
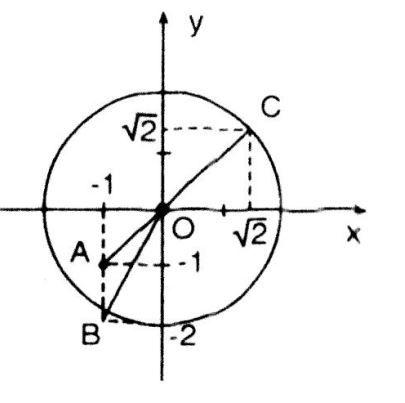

Trong mặt phẳng tọa độ Oxy, vẽ đường tròn
Vị trí các điểm A, B, C được xác định như hình vẽ.
Thật vậy :
Ta có:
Vậy điểm A nằm bên trong (O).
Ta có:
Vậy điểm B nằm bên ngoài đường tròn (O).
Ta có:
Vậy điểm C nằm trên đường tròn (O).
Bài 5. (Trang 100 SGK Toán 9 – Tập 1)
Đố. Một tấm bìa hình tròn không còn dấu vết của tâm. Hãy tìm lại tâm của hình tròn đó.
Bài giải
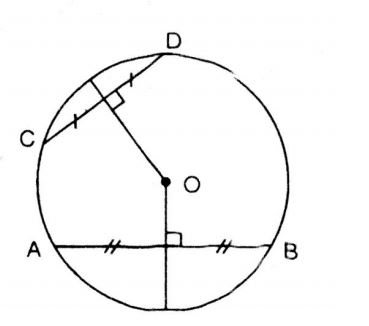

Ta xác định tâm của đường tròn bằng cách:
Vẽ hai dây AB và CD bất kì của đường tròn. Vẽ hai đường trung trực của chúng. Giao điểm hai đường trung trực của hai dây đó là tâm của đường tròn cần tìm.
Bài 6. (Trang 100 SGK Toán 9 – Tập 1)
Trong các biển báo giao thông sau, biển nào có tâm đối xứng, biển nào có trục đối xứng ?
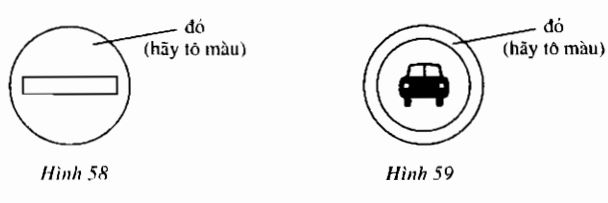
a) Biển cấm đi ngược chiều (h.58)
b) Biển cấm ô tô (h.59).

Bài giải
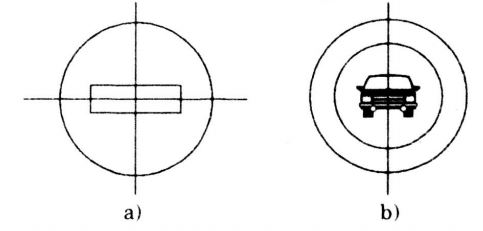
a) Hình a: Biển cấm đi ngược chiều có một tâm đối xứng (tâm đường tròn) và có hai trục đối xứng (là hai đường kính đi qua trung điểm các cạnh đối của hình chữ nhật).
b) Biển cấm ô tô chỉ có trục đối xứng.

Bài 7. (Trang 101 SGK Toán 9 – Tập 1)
Hãy nối mỗi ô ở cột trái với mỗi ô ở cột phải để được khẳng định đúng :
| (1) Tập hợp các điểm có khoảng cách đến điểm A cố định bằng 2 cm | (4) là đường tròn tâm A bán kính 2cm |
| (2) Đường tròn tâm A bán kính 2cm gồm tất cả những điểm | (5) có khoảng cách đến điểm A nhỏ hơn hoặc bằng 2cm |
| (3) Hình tròn tâm A bán kính 2cm gồm tất cả những điểm | (6) có khoảng cách đến điểm A bằng 2cm |
| (7) có khoảng cách đến điểm A lớn hơn 2cm |
Bài giải
Ta nối các ý: (1) và (4); (2) và (6); (3) và (5) sẽ được câu đúng
Bài 8. (Trang 101 SGK Toán 9 – Tập 1)
Cho góc nhọn xAy và hai điểm B, C thuộc tia Ax. Dựng đường tròn (O) đi qua B và C sao cho tâm O nằm trên tia Ay.
Bài giải
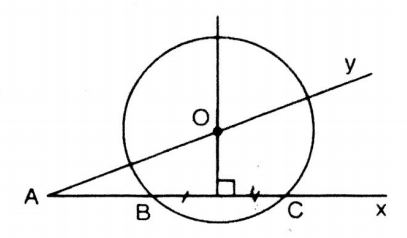

Giả sử ta dựng được đường tròn (O) thỏa mãn điều kiện của đề bài.
Dựng góc xAy, trên tia Ax lấy hai điểm B và C.
Dựng đường trung trục đoạn BC, cắt tia Ay tại O.
Ta được O là tâm đường tròn đi qua hai điểm B và C.
Thật vậy, O là giao điểm của tia Ay với đường trung trực của đoạn BC nên OB = OC. Điều này chứng tỏ rằng hai điểm B và C nằm trên đường tròn (O).
Vậy tâm O là giao điểm của tia Ay với đường trung trực của BC
Bài 9. (Trang 101 SGK Toán 9 – Tập 1)
Đố
a) Vẽ hình hoa bốn cánh. Hình hoa bốn cánh trên hình 60 được tạo bởi các cung có tâm A, B, C, D (trong đó A, B, C, D là các đỉnh của một hình vuông và tâm của cung là tâm của đường tròn chứa cung đó). Hãy vẽ lại hình 60 vào vở
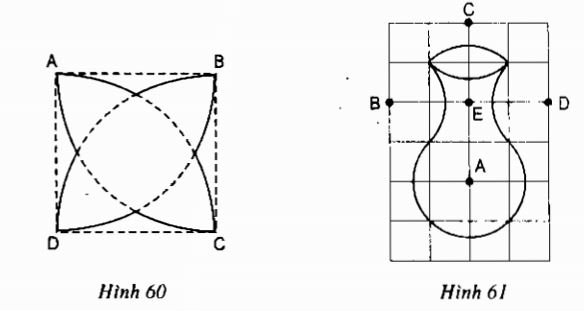

b) Vẽ lọ hoa: Chiếc lọ hoa trên hình 61 được vẽ trên giấy kẻ ô vuông bởi năm cung có tâm A, B, C, D, E. Hãy vẽ lại hình 61 vào giấy kẻ ô vuông.
Bài giải
a) Cách vẽ:
- Vẽ hình vuông ABCD
- Vẽ cung tròn tâm A, bán kính là cạnh hình vuông. Cung tròn này đi qua B, D
- Tương tự với các cung tròn còn lại
- Ta được bốn cung tròn tạo thành hình hoa bốn cánh.
b) Cách vẽ:
- Kẻ các ô vuông và lấy điểm như hình 61
- Lần lượt vẽ các cung tròn có tâm là các điểm A, B, C, D, E và bán kính là đường chéo của ô vuông.
- Ta được 5 cung tròn liền nét vói nhau tạo thành hình chiếc lọ hoa
Xem thêm hướng dẫn giải bài tập sách giáo khoa toán 9: Đường kính và dây của đường tròn

