8.3. Hình cầu. Diện tích mặt cầu và thể tích hình cầu

Hướng dẫn giải bài tập sgk toán lớp 9 tập 2 trang 124-126. Hình cầu. Diện tích mặt cầu và thể tích hình cầu

Bài 30. (Trang 124 SGK Toán 9 – Tập 2)

Nếu thể tích của một hình cầu là thì trong các kết quả sau đây, kết quả nào là bán kính của nó (lấy ) ?

Bài giải

Áp dụng công thức với để tính R.

Ta có:

Vậy chọn câu (B).

Bài 31. (Trang 124 SGK Toán 9 – Tập 2)

Hãy điền vào các ô trống ở bảng sau :

Bán kính hình cầu	0,3 mm	0,61 dm	0,283 m	100 km	6 hm	50 dam
Diện tích mặt cầu
Thể tích hình cầu

Bài giải

Áp dụng các công thức tính S và v với:

Ta có kết quả

Bán kính hình cầu	0,3 mm	0,61 dm	0,283 m	100 km	6 hm	50 dam
Diện tích mặt cầu
Thể tích hình cầu

Bài 32. (Trang 125 SGK Toán 9 – Tập 2)

Một khối gỗ dạng hình trụ, bán kính đường tròn đáy là r, chiều cao 2r (đơn vị : cm). Người ta khoét rỗng hai nửa hình cầu như hình 108. Hãy tính diện tích bề mặt của khối gỗ còn lại (diện tích cả ngoài lẫn trong).

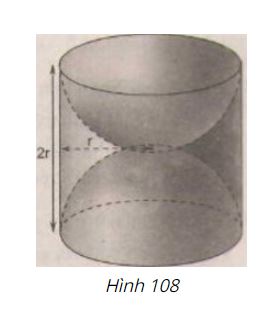
Bài giải

Theo đề bài ta có: Diện tích phần cần tính gồm diện tích xung quanh của hình trụ (bán kính đường tròn đáy là r (cm); chiều cao là 2r (cm)).

Ta có:

Diện tích xung quanh hình trụ là:

Tổng diện tích hai nửa mặt cầu là:

Vậy diện tích cần tính là:

Vậy

Bài 33. (Trang 125 SGK Toán 9 – Tập 2)

Dụng cụ thể thao

Các loại bóng cho trong bảng đều có dạng hình cầu. Hãy điền vào các ô trống ở bảng sau (làm tròn kết quả đến chữ số thập phân thứ hai) :

Loại bóng	Quả bóng gôn	Quả khúc côn cầu	Quả ten nít	Quả bóng bàn	Quả bi-a
Đường kính	42,7 mm		6,5 cm	40 mm	61 mm
Độ dài đường tròn lớn		23 cm
Diện tích
Thể tích

 

Bài giải

Loại bóng	Quả bóng gôn	Quả khúc côn cầu	Quả ten nít	Quả bóng bàn	Quả bi-a
Đường kính	42,7 mm	7,32 cm	6,5 cm	40 mm	61 mm
Độ dài đường tròn lớn	134,08 mm	23 cm	20,41 cm	125,6 mm	191,54 mm
Diện tích
Thể tích

 

Bài 34. (Trang 125 SGK Toán 9 – Tập 2)

Khinh khí cầu của nhà Mông-gôn-fi-ê

Ngày 4- 6 – 1783, anh em nhà Mông – gôn – fi – ê (người Pháp) phát ra khinh khí cầu dùng không khí nóng. Coi khinh khí cầu này là hình cầu này là hình cầu có đường kính 11 m. Hãy tính diện tích mặt khinh khí cầu đó (làm tròn kết quả đến chữ số thập phân thứ hai).

Bài giải

Ta có diện tích mặt cầu tính theo công thức:

Bài 35. (Trang 126 SGK Toán 9 – Tập 2)

Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ (h.110).

Hãy tính thể tích của bồn chứa theo các kích thước cho trên hình vẽ.

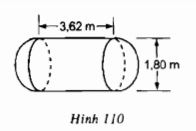
Bài giải

Theo đề bài cho, thể tích hình cầu cần tính bằng tổng thể tích của hình trụ và thể tích của một hình cầu có đường kính bằng 1,8 m. Ta có:

Thể tích hình trụ là:

Thể tích hình cầu là:

Vậy thể tích bồn xăng là:

Bài 36. (Trang 126 SGK Toán 9 – Tập 2)

Một chi tiết máy gồm một hình trụ và hai nửa hình cầu với các kích thước đã cho trên hình 111 (đơn vị : cm)

a) Tìm một hệ thức giữa x và h khi AA’ có độ dài không đổi và bằng 2a.

b) Với điều kiện ở a), hãy tính diện tích bề mặt và thể tích của chi tiết máy theo x và a.

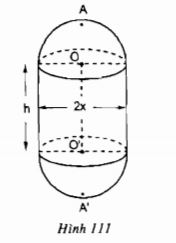
Bài giải

a) Theo đề bài và nhìn hình vẽ ta có: Hai nửa mặt cầu đều có bán kính bằng x. Như vậy đường kính hình cầu sẽ là 2x. Do đó ta có hệ thức:

Vậy hệ thức là hệ thức cần tìm.

b) Theo đề bài thì diện tích bề mặt chi tiết máy bằng tổng diện tích hình trụ và hình cầu. Do đó:

Tương tự cho thể tích chi tiết máy

Bài 37. (Trang 126 SGK Toán 9 – Tập 2)

Cho nửa đường tròn tâm O, đường kính , Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.

a) Chứng minh rằng MON và APB là hai tam giác vuông đồng dạng

b) Chứng minh

c) Tính tỷ số khi

d) Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.

Bài giải

a) Xét hai tam giác vuông MON và APB, ta có:

(tính chất hai tiếp tuyến)

(góc có cạnh tương ứng vuông góc)

Suy ra:

Vậy đồng dạng (c.c)

b) Ta có: (tính chất hai tiếp tuyến) (1)

Áp dụng hệ thức lượng trong tam giác vuông OMN, ta có:

Từ (1) và (2), ta có: .

c) Vì đồng dạng nên ta có:   (3)

Khi và , suy ra

Do đó:

Suy ra

Thế vào (3), ta có:

d) Vì nửa hình tròn APB quay quanh đường kính AB tạo ra một hình cầu bán kính R. Khi đó thể tích hình cầu là:

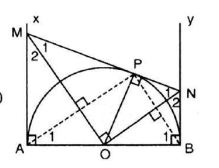
Xem thêm hướng dẫn giải bài tập sgk toán 9. Ôn tập chương VIII