7.7. Tứ giác nội tiếp
Hướng dẫn giải bài tập sgk toán lớp 9 tập 2 trang 89-90. Bài học: Tứ giác nội tiếp
Nội dung chính
Bài 53. (Trang 89 SGK Toán 9 – Tập 2)
Biết ABCD là tứ giác nội tiếp. Hãy điền vào ô trống trong bảng sau: (nếu có thể):
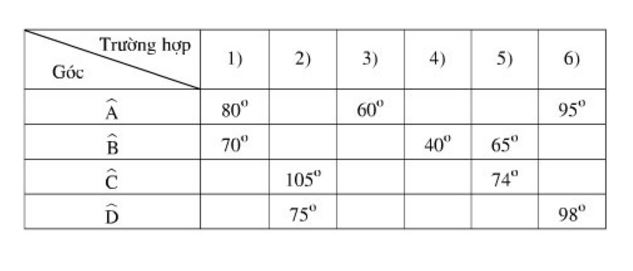
Bài giải
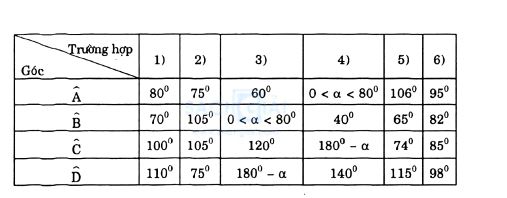
Ví dụ: Trường hợp 1: Vì ABCD nội tiếp (O) nên 
Bài 54. (Trang 89 SGK Toán 9 – Tập 2)
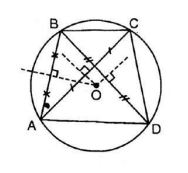
Tứ giác ABCD có 
. Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm.
Bài giải
Tứ giác ABCD có (hai góc đối diện) nên nội tiếp được trong đường tròn. Gọi O là tâm đường tròn đó. Vì O là tâm đường tròn ngoại tiếp tứ giác ABCD nên:
Ta có: 
nên đường trung trực của AC đi qua O
Ta có: 
nên đường trung trực của BD đi qua O
Ta có: 
nên đường trung trực của AB đi qua O.
Tóm lại các đường trung trực của AC, BD và AB cùng đi qua O.
Bài 55. (Trang 89 SGK Toán 9 – Tập 2)
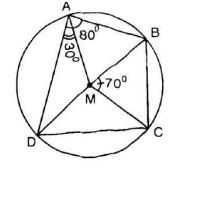
Cho ABCD là tứ giác nội tiếp đường tròn tâm M, biết 
, 
.
Hãy tính số đo các góc 
Bài giải
Ta có: 
Ta có tam giác MBC cân tại M (
)
Nên 
Ta có tam giác MAB cân 
nên 
Ta có tam giác MAD cân 
nên
Ta có: 
Suy ra: 
Ta có: 
(do ABCD nội tiếp)
Bài 56. (Trang 89 SGK Toán 9 – Tập 2)
Xem hình 47. Hãy tìm số đo các góc trong tứ giác ABCD.
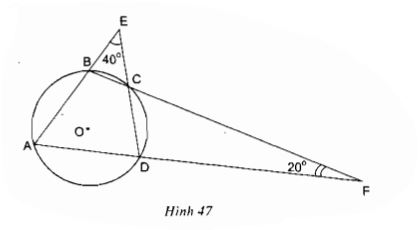
Bài giải
Ta có: 
(đối đỉnh)
Đặt 
Áp dung tính chất góc ngoài của tam giác BCE và DCF, ta có:
Vì tứ giác ABCD nội tiếp trong (O) nên:
Thế vào (1), ta được: 
Thế vào (2), ta được: 
Ta có: 
(hai góc kề bù)
Ta có: 
(tứ giác nội tiếp)
Bài 57. (Trang 89 SGK Toán 9 – Tập 2)
Trong các hình sau, hình nào nội tiếp được trong một đường tròn:
Hình bình hành, hình chữ nhật, hình vuông, hình thang, hình thang vuông, hình thang cân ? Vì sao ?
Bài giải
Tổng quát: Hình bình hành không nội tiếp được trong đường tròn vì tổng hai góc đối diện không bằng 
Hình chữ nhật, hình vuông nội tiếp được trong đường tròn, vì tổng hai góc đối diện bằng
Hình thang vuông không nội tiếp được trong đường tròn.
Tổng quát hình thang không nội tiếp được trong đường tròn. Riêng hình thang cân nội tiếp được trong đường tròn vì tổng hai góc đối diện bằng .
Bài 58. (Trang 90 SGK Toán 9 – Tập 2)
Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho 
và 
.
a) Chứng minh ABDC là tứ giác nội tiếp.
b) Xác định tâm đường tròn đi qua bốn điểm A, B, D, C.
Bài giải
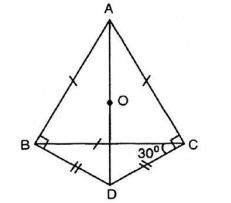
a) Theo đề bài ta có:
Vậy 
Vì tam giác cân tại D 
nên 
.
Vậy 
Xét tứ giác ABDC, ta có: 
Vậy tứ giác ABDC nội tiếp được.
b) Vì 
nên 
là góc nội tiếp chắn nửa đường tròn đường kính AD, tâm O là trung điểm của AD.
Tương tự, 
, nên 
là góc nội tiếp chắn nửa đường tròn đường kính AD.
Vậy tứ giác ABDC nội tiếp trong đường tròn đường kính AD, tâm O là trung điểm của AD.
Bài 59. (Trang 90 SGK Toán 9 – Tập 2)
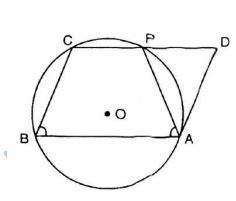
Cho hình bình hành ABCD. Đường tròn đi qua ba đỉnh A, B, C cắt đường thẳng CD tại P khác C. Chứng minh 
Bài giải
Theo đề bài, tứ giác ABCP nội tiếp, nên ta có:
Ta có: 
(hai góc kề bù)
So sánh (1) và (2), ta có: 
.
Mặt khác 
(hai góc đối đỉnh của hình bình hành ABCD).
Suy ra 
Vậy tam giác PAD cân tại A. Suy ra 
Bài 60. (Trang 90 SGK Toán 9 – Tập 2)
Xem hình 48. Chứng minh 
Hướng dẫn. Xét cặp góc so le trong 
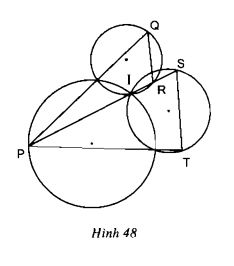
Bài giải
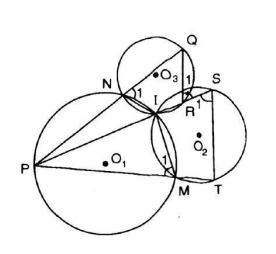
Tứ giác SIMT nội tiếp trong 
nên:
Mà 
(kề bù)
nên 
Tương tự, tứ giác PMIN nội tiếp trong 
nên:
(2)
Tương tự, trong tứ giác NQRI, ta có: 
(3)
Từ (1) (2) (3) suy ra : 
(hai góc 
và 
ở vị trí so le trong).
Vậy 
Xem thêm hướng dẫn giải bài tập sgk toán 9. Đường tròn ngoại tiếp, đường tròn nội tiếp.
Bạn có thể in hoặc xuất file pdf! Thật tuyệt!
