2.5. Hệ số góc của đường thẳng y = ax + b (a khác 0) và Luyện tập

Hướng dẫn giải bài tập sgk trang 58 . Bài học Hệ số góc của đường thẳng y = ax + b (a khác 0) và Luyện tập.

Bài 27. (Trang 58 SGK Toán 9 – Tập 1)

Cho hàm số bậc nhất .

a) Xác định hệ số góc , biết rằng đồ thị của hàm số đi qua điểm

b) Vẽ đồ thị của hàm số.

Bài giải

a) Vì đồ thị của hàm số đi qua điểm A(2;6) nên tọa độ điểm A nghiệm đúng phương trình:

Ta được hàm số

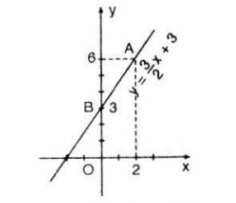b) Vẽ đồ thị hàm số .

-Cho , tính được . Ta xác định được điểm

-Cho , tính được . Ta xác định được điểm

Đồ thị hàm số là đường thẳng đi qua hai điểm .

Bài 28. (Trang 58 SGK Toán 9 – Tập 1)

Cho hàm số  y = -2x +3

a) Vẽ đồ thị của hàm số.

b)Tính góc tạo bởi đường thẳng y = -2x +3 và trục Ox ( làm tròn đến phút).

Bài giải

a) Vẽ đồ thị hàm số -Cho , tính được . Ta xác định được điểm . -Cho y = 0, tính được . Ta xác định được điểm Đồ thị hàm số là đường thẳng đi qua hai điểm .

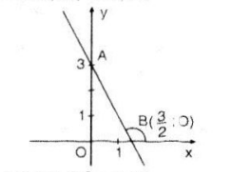b) Gọi là góc tạo bởi đường thẳng   và trục , ta có:

.

Xét tam giác vuông AOB có:

Suy ra: .

Vậy .

Bài 29. (Trang 59 SGK Toán 9 – Tập 1)

Xác định hàm số bậc nhất trong mỗi trường hợp sau:

a) và đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng

b) và đồ thị của hàm số đi qua điểm

c) Đồ thị của hàm số song song với đường thẳng và đi qua điểm .

Bài giải

a) Thay a = 2 vào hàm số ,ta được .

Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng nghĩa là điểm có tọa độ

Thay tọa độ vào (1), ta được:

Vậy hàm số tìm được là:  .

b)Thay vào hàm số , ta được .

Đồ thị đi qua điểm (2;2) nên tọa độ (2;2) nghiệm đúng phương trình (2), nghĩa là:

Vậy hàm số tìm được là: .

c) Vì đồ thị của hàm số song song với đường thẳng  nên .

Thay vào ta được hàm số .

Vì đường thẳng (3) đi qua điểm nên tọa độ ( là nghiệm đúng phương trình nghĩa là:

Vậy hàm số tìm được : .

Bài 30. (Trang 59 SGK Toán 9 – Tập 1)

a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hàm số sau:

b) Gọi giao điểm của hai đường thẳng và với trục hoành theo thứ tự là và gọi giao điểm của hai đường thẳng đó là C.

Tính các góc của tam giác (làm tròn đến độ).

c) Tính chu vi và diện tích của tam giác (đơn vị đo trên các trục tọa độ là xentimet).

Bài giải

a) Vẽ đồ thị các hàm số:

*

-Cho , tính được Ta xác định được điểm .

-Cho , tính được Ta xác định được điểm.

A(-4;0). Đồ thị hàm số   là đường thẳng đi qua hai điểm A và C. * -Cho , tính được . Ta xác định được điểm . -Cho , tính được . Ta xác định được điểm . Đồ thị hàm số là đường thẳng đi qua hai điểm và

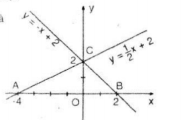b) Tính các góc của tam giác

• Ta có: .

Suy ra

• Ta có: . Suy ra
• Ta có:

hay

c) Tính chu vi và diện tích :

• Ta có ; .

Khi đó:

Chu vi

Diện tích

Bài 31. (Trang 59 SGK Toán 9 – Tập 1)

a) Vẽ đồ thị của các hàm số lần lượt là các góc tạo bởi các đường thẳng trên và trục

Chứng minh: .

Tính số đo các góc .

Bài giải

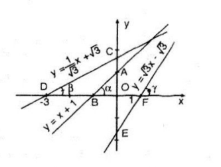
*Vẽ đồ thị hàm số:

-Hàm số

Đồ thị hàm số là một đường thẳng đi qua hai điểm A(0;1) và

• Hàm số

Đồ thị hàm số là một đường thẳng đi qua hai điểm và

• Hàm số

Đồ thị hàm số là một đường thẳng đi qua hai điểm và F(1;0).

*Chứng minh

• Với hàm số

ta có: -Với hàm số , ta có: -Với hàm số ta có:

Xem thêm Hướng dẫn giải bài tập sgk toán lớp 9 Ôn tập chương II