5.8. Đối xứng tâm
Nội dung chính
ÔN TẬP: ĐỐI XỨNG TÂM
![]() KIẾN THỨC CẦN NHỚ
KIẾN THỨC CẦN NHỚ

 BÀI TẬP VÍ DỤ
BÀI TẬP VÍ DỤ
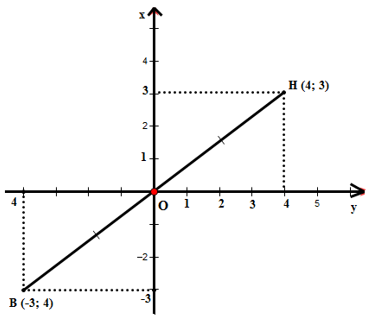
Ví dụ 1: Trong mặt phẳng tọa độ, cho điểm A có tọa độ (4; 3). Hãy vẽ điểm B đối xứng với H qua gốc tọa độ và tìm tọa độ của B.
Bài giải:
Ví dụ 2: Trong các hình sau, hình nào có tâm đối xứng?
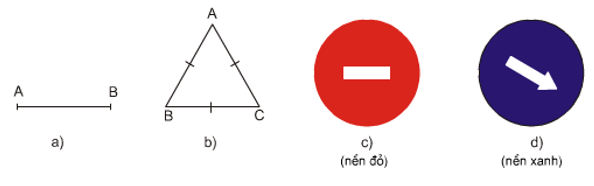
Bài giải:
Hình a, hình c có tâm đối xứng.
Hình a có tâm đối xứng là trung điểm của đoạn thẳng AB.
Hình c có tâm đối xứng là tâm của đường tròn.
 BÀI TẬP VẬN DỤNG
BÀI TẬP VẬN DỤNG
 BÀI TẬP CƠ BẢN
BÀI TẬP CƠ BẢN
Bài 1: Cho ABCD là hình bình hành. Chứng minh rằng điểm M đối xứng với điểm N qua C.
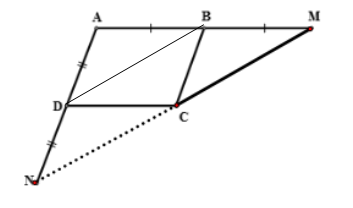
Bài giải:
Tứ giác BMCD có BM // CD, BM = CD nên BMCD là hình bình hành.
Suy ra CM // BD, CM = BD. (1)
Tứ giác BCND có BC // DN, BC = DN nên BCND là hình bình hành.
Suy ra CN // BD, CN = BD. (2)
Từ (1), (2) suy ra M, C, N thẳng hàng và CM = CN. Do đó M đối xứng với N qua C.
Bài 2: Các điểm và
đối xứng với các điểm
và
qua điểm
Bài giải:
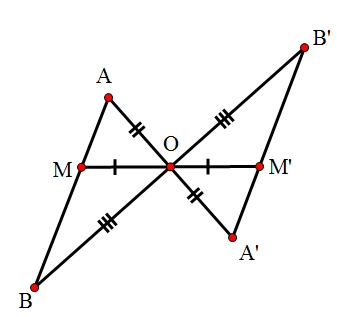

Theo định lí về hai đoạn thẳng đối xứng với nhau qua điểm
Do
Vậy
Ta có:
Với:
![]()
![]()
Bài 1: Cho tam giác ABC, các đường trung tuyến BM, CN. Gọi D là điểm đối xứng với B qua M, gọi E là điểm đối xứng với C qua N. Chứng minh rằng các điểm D đối xứng với điểm E qua điểm A.
Bài giải:
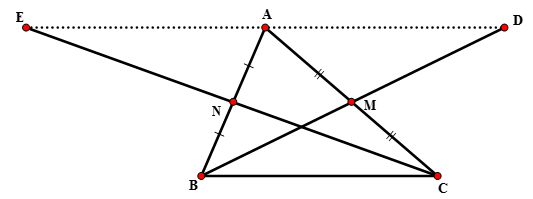

Tứ giác ABCD có các đường chéo cắt nhau tại trung điểm của mỗi đường:
MA = MC, MB = MD nên ABCD là hình bình hành.
Suy ra AD // BC, AD = BC. (1)
Tứ giác AEBC có các đường chéo cắt nhau tại trung điểm của mỗi đường:
NA = NB, NE = NC nên AEBC là hình bình hành.
Suy ra AE // BC, AE = BC. (2)
Từ (1), (2) suy ra D, A, E thẳng hàng và AD = AE. Do đó D đối xứng với E qua A.
Bài 2: Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. E là trung điểm của OD. M là điểm đối xứng của C qua E. N đối xứng với M qua A.Chứng minh rằng N và C đối xứng nhau qua trung điểm của OB.
Bài giải:
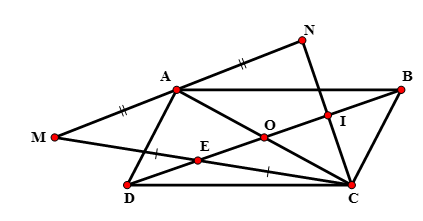

Gọi giao điểm của NC và OB tại I.
E là trung điểm OD nên OE = ED.
Xét tam giác ACM có EO là đường trung bình nên EO // MA,
Xét tam giác ANC có O là trung điểm AC, OI // AN suy ra I là trung điểm của NC.
Và
Vì AM = AN và từ (1), (2) ta suy ra OI = IB suy ra I là trung điểm của OB. Vậy N và C đối xứng nhau qua trung điểm OB.
Chúc các em học tập hiệu quả!

