7.1. Định lí Ta – lét trong tam giác
Nội dung chính
ÔN TẬP: ĐỊNH LÍ TA-LÉT TRONG TAM GIÁC
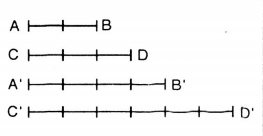
![]() KIẾN THỨC CẦN NHỚ
KIẾN THỨC CẦN NHỚ
 BÀI TẬP VÍ DỤ
BÀI TẬP VÍ DỤ
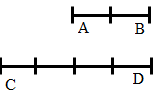
Ví dụ 1: Cho biết và
Tính độ dài AB.
Bài giải:
Ví dụ 2: Tính độ dài trong hình bên, biết rằng:
.
Bài giải:
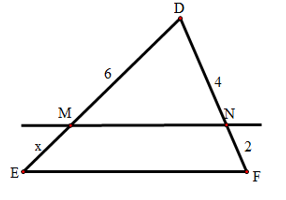
Vì .
 BÀI TẬP VẬN DỤNG
BÀI TẬP VẬN DỤNG
 BÀI TẬP CƠ BẢN
BÀI TẬP CƠ BẢN
Bài 1: Gọi là điểm nằm trên đoạn thẳng
sao cho
.
Tính các tỉ số và
.
Bài giải:
Áp dụng tính chất của tỉ lệ thức và tính chất dãy tỉ số bằng nhau, ta có:
.
Suy ra: và
.
Bài 2: Cho hình vẽ dưới, . Tính độ dài AC.
Bài giải:
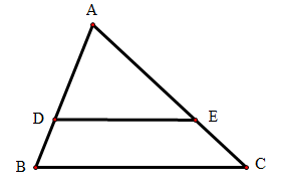
Ta có .
 BÀI TẬP NÂNG CAO
BÀI TẬP NÂNG CAO
Bài 1: Cho tam giác ABC có AB = 9cm, điểm D thuộc cạnh AB sao cho AD = 6cm. Kẻ DE song song với BC , kẻ EF song song với CD
. Tính độ dài AF.
Bài giải:
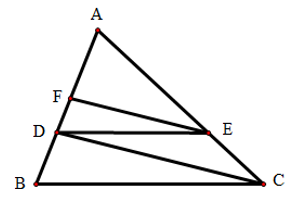
Áp dụng định lí Ta-lét với EF // CD, ta có , với DE // BC, ta có
.
Suy ra , tức là
.
Vậy .
Bài 2: Cho tam giác ABC. M là điểm bất kì trên BC. Vẽ đường thẳng MN song song với AC (N thuộc AB), đường thẳng MP song song với AB (P thuộc AC). Chứng minh .
Bài giải:
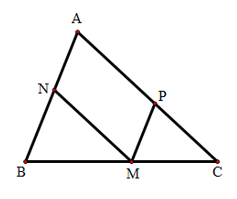
Ta có (giả thiết)
(1) (Định lí Ta-lét)
Tương tự (2)
Từ (1) và (2)
Xem thêm: Định lí đảo và hệ quả của định lý Ta-let
Chúc các em học tập hiệu quả!

