7.3. Tính chất đường phân giác của tam giác
Nội dung chính
ÔN TẬP: TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC
![]() KIẾN THỨC CẦN NHỚ
KIẾN THỨC CẦN NHỚ
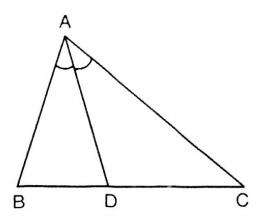
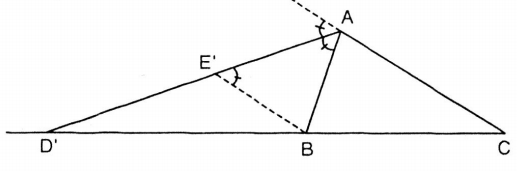
 BÀI TẬP VÍ DỤ
BÀI TẬP VÍ DỤ
Ví dụ 1: Cho có
Tính độ dài đoạn DC.
Bài giải:
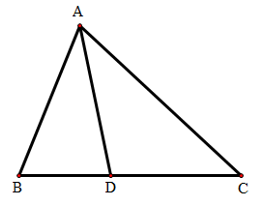
Theo giải thiết
.
 BÀI TẬP VẬN DỤNG
BÀI TẬP VẬN DỤNG
 BÀI TẬP CƠ BẢN
BÀI TẬP CƠ BẢN
Bài 1: Tam giác ABC có AB = 6cm, AC = 9cm, BC = 10cm, đường phân giác trong AD, đường phân giác ngoài AE. Tính các độ dài DB, EB.
Bài giải:
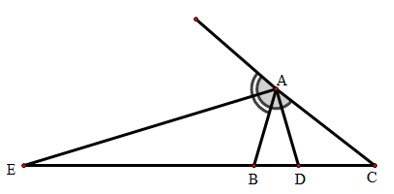
Từ , ta tính được DB = 4cm; EB = 20cm.
Bài 2: Cho tam giác ABC cân tại A, AB = 10cm, BC = 12cm. Gọi I là giao điểm các đường phân giác của tam giác. Tính độ dài AI.
Bài giải:
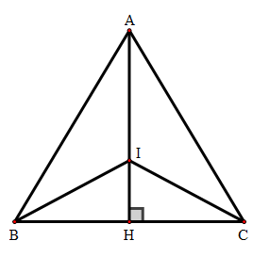
Gọi H là giao điểm của AI và BC. Tam giác ABC cân tại A nên đường phân giác AH cũng là đường cao.
Theo định lí Py- ta- go, ta có: nên AH = 8cm.
Theo tính chất đường phân giác
nên
, tức là
hay
.
Vậy .
![]() BÀI TẬP NÂNG CAO
BÀI TẬP NÂNG CAO
Bài 1: Cho tam giác ABC có AM là trung tuyến, các đường phân giác của góc BMA và góc CMA cắt AB, AC tương ứng tại D và E.
a) Chứng minh rằng DE // BC.
b) Gọi O là giao điểm của AM và DE. Chứng minh OD = OE.
Bài giải:
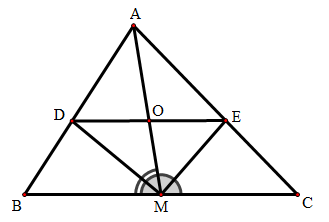
a) DM là đường phân giác của nên theo tính chất đường phân giác của tam giác ta có
(1)
Tương tự EM là đường phân giác nên
(2)
Mà MB = MC nên từ (1) và (2) (định lí Ta lét đảo)
b) mà
và
.
Do đó mà BM = CM (giả thiết)
.
Bài 2: Chứng minh rằng nếu một đường thẳng đi qua một đỉnh của một tam giác mà chia cạnh dối diện thành hai đoạn tỉ lệ với hai cạnh kề hai đoạn ấy thì nó là đường phân giác trong (hoặc ngoài) của góc tại đỉnh ấy.
Bài giải:
a)
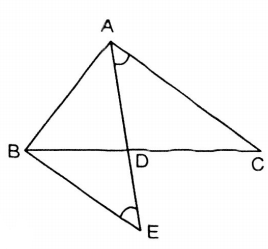
Giả sử là điểm chia trong của cạnh
Ta đi chứng minh
Qua
Theo hệ quả của định lí Ta-lét trong
Mà
Mặt khác:
Do
b)
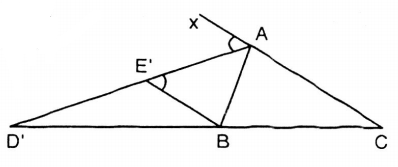

Giả sử điểm
Kẻ
Theo hệ quả của định lí Ta – lét trong
Từ (1)(2)
Mặt khác:
Do
Xem thêm: Khái niệm hai tam giác đồng dạng
Chúc các em học tập hiệu quả!

