5.7. Hình bình hành
ÔN TẬP: HÌNH BÌNH HÀNH
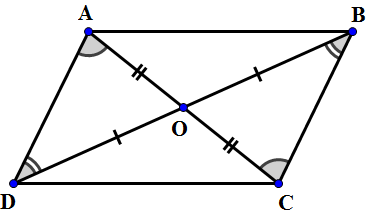
![]() KIẾN THỨC CẦN NHỚ
KIẾN THỨC CẦN NHỚ
 BÀI TẬP VÍ DỤ
BÀI TẬP VÍ DỤ
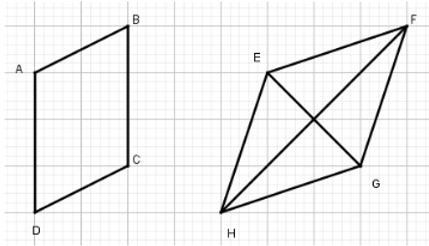
Ví dụ 1: Các hình trên giấy kẻ ô vuông dưới đây có là hình bình hành không?
Bài giải:
Tứ giác ABCD là hình bình hành vì có cạnh đối AD // BC và AD = BC bằng 3 cạnh ô vuông.
Tứ giác EFGH là hình bình hành vì có các cạnh đối bằng nhau.
EH = FG là đường chéo hình chữ nhật có cạnh 1 ô vuông và cạnh 3 ô vuông
EF = HG là đường chéo hình chữ nhật có cạnh 1 ô vuông và cạnh 3 ô vuông.
Ví dụ 2: Cho tam giác ABC có , H là trực tâm. Đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở điểm I. Chứng minh rằng BICH là hình bình hành.
Bài giải:
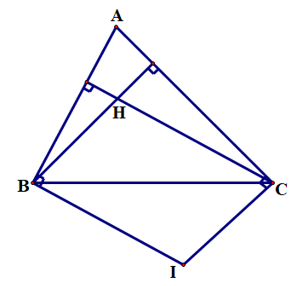
Vì H là trực tâm của nên
và
.
Mà và
và
là hình bình hành do có hai cặp cạnh đối song song.
 BÀI TẬP VẬN DỤNG
BÀI TẬP VẬN DỤNG
 BÀI TẬP CƠ BẢN
BÀI TẬP CƠ BẢN
Bài 1: Cho hình bình hành ABCD là hình bình hành. Kẻ và
. Chứng minh AECF là hình bình hành.
Bài giải:
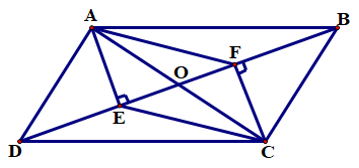
Gọi O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD.
(1)
Xét hai tam giác vuông AEO và CFO, ta có: .
Do đó (cạnh huyền – góc nhọn)
(2)
Từ (1) và (2) suy ra tứ giác AECF là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Bài 2: Cho hình bình hành ABCD (AB > BC), phân giác của góc D cắt AB tại M, phân giác của góc B cắt CD tại N.
a) Chứng minh rằng AM = CN.
b) Chứng minh: Tứ giác DMBN là hình bình hành.
Bài giải:
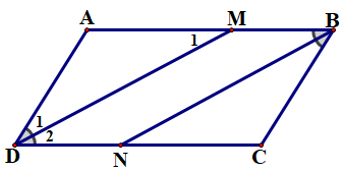
a) Vì ABCD là hình bình hành nên AB // CD (so le trong) mà
hay tam giác AMD cân tại A
(1)
Chứng minh tương tự ta có tam giác BNC cân tại C (2)
Mà ABCD là hình bình hành nên AD = BC. (3)
Từ (1), (2) và (3) suy ra AM = CN.
b) ABCD là hình bình hành suy ra AB = CD.
Lại có hay BM = DN.
Mặt khác BM // DN do đó tứ giác DMBN là hình bình hành.
 BÀI TẬP NÂNG CAO
BÀI TẬP NÂNG CAO
Bài 1: Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?
Bài giải:
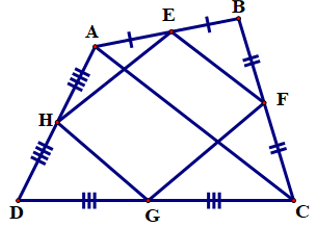
Nối đường chéo AC.
Trong tam giác ABC ta có: E, F lần lượt là trung điểm của AB, BC nên EF là đường trung bình của tam giác ABC.
(1)
Trong tam giác ADC có: H, G lần lượt là trung điểm của AD, DC nên HG là đường trung bình của tam giác ADC.
(2)
Từ (1) và (2) suy ra: EF // HG và EF = HG.
Vậy tứ giác EFGH là hình bình hành vì có một cặp cạnh đối song song và bằng nhau.
Bài 2: Cho hình bình hành , đường phân giác của góc
cắt
tại
a) Chứng minh
b) Phân giác của góc cắt
tại
Chứng minh rằng
là hình bình hành.
Bài giải:
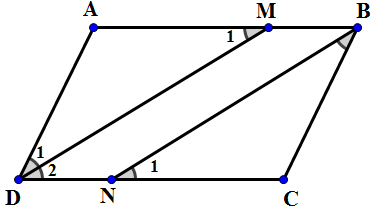
a) Ta có: .
và
so le trong.
và
Xét có
Suy ra:
b) Ta có:
và
Vậy
Chúc các em học tập hiệu quả!

