6.5. Diện tích hình thoi

ÔN TẬP: DIỆN TÍCH HÌNH THOI

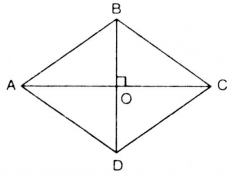
BÀI TẬP VÍ DỤ

Ví dụ 1: Cho hình thoi ABCD có AC = 10cm, BD = 6cm. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tính diện tích tứ giác EFGH.

Bài giải:

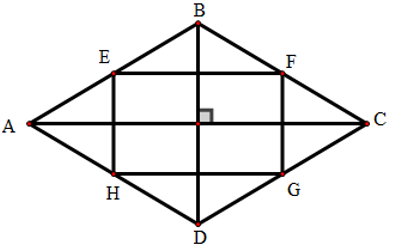
Sử dụng các tính chất đường trung bình của tam giác, ta chứng minh EFGH là hình chữ nhật.

Từ đó suy ra:

Ví dụ 2: Tính diện tích hình thoi ABCD cạnh 8cm, .

Bài giải:

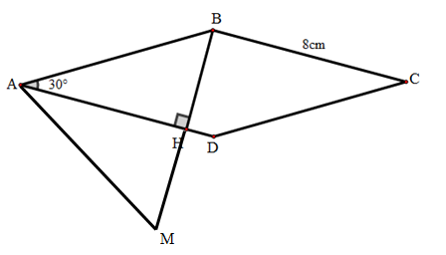
Kẻ . Xét vuông tại H có

Để chứng minh ta vẽ điểm M là điểm đối xứng của B qua H. Khi đó tam giác ABM là tam giác đều suy ra H là trung điểm của BM.

Diện tích hình thoi ABCD là:

BÀI TẬP VẬN DỤNG

BÀI TẬP CƠ BẢN

Bài 1: Một hình chữ nhật có diện tích . Tính diện tích tứ giác có bốn đỉnh là bốn trung điểm của bốn cạnh hình chữ nhật đã cho.

Bài giải:

Gọi hình chữ nhật là ABCD.

M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA.

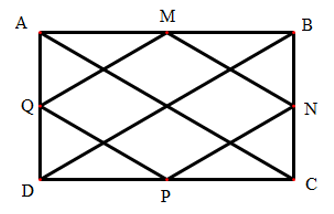
Sử dụng các tính chất đường trung bình của tam giác.

Xét tam giác ABC có:

Xét tam giác ADC có:

là hình bình hành.

Mặt khác Xét tam giác ABD có: (tính chất hình chữ nhật)

Suy ra MN = MQ.

Vậy MNPQ là hình  thoi. Khi đó, ta tính được:

Bài 2: 

BÀI TẬP NÂNG CAO

Bài 1: Tính diện tích hình thoi, biết cạnh của nó dài 6,2cm và một trong các góc của nó có số đo .

Bài giải: 

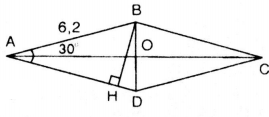
Cho hình thoi . Từ kẻ .

Xét tam giác vuông có do đó có thể xem là nửa tam giác đều cạnh

Mà

Đáp số:

Bài 2: Cho tam giác ABC cân, AB = AC = 5cm, BC = 6cm. G là trọng tâm của tam giác ABC. Lấy D đối xứng với G qua BC.

a) Chứng minh rằng tứ giác BDCG là hình thoi.

b) Tính diện tích tứ giác BDCG.

Bài giải:

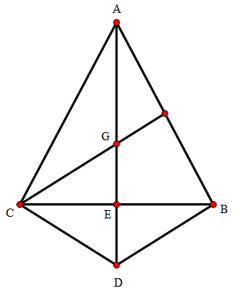
a) Gọi giao điểm của AG với CB là E. Vì G là trọng tâm nên AE là trung tuyến hay E là trung điểm của BC.

Mặt khác D đối xứng với G qua BC nên tại E’ là trung điểm của GD.

Mà cân tại A nên AE cũng là trung trực của BC

thẳng hàng.

Tứ giác GCDB có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành, lại có hai đường chéo vuông góc nên nó là hình thoi. Vậy tứ giác BDCG là hình thoi.

b)

Vì BDCG là hình thoi nên

Xem thêm: Diện tích đa giác