6.2. Diện tích hình chữ nhật
Nội dung chính
ÔN TẬP: DIỆN TÍCH HÌNH CHỮ NHẬT
![]() KIẾN THỨC CẦN NHỚ
KIẾN THỨC CẦN NHỚ
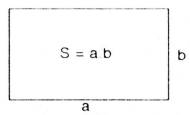
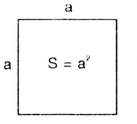
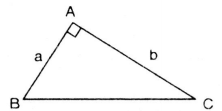
 BÀI TẬP VÍ DỤ
BÀI TẬP VÍ DỤ
Ví dụ 1: Diện tích một hình vuông tăng thêm bao nhiêu phần trăm nếu mỗi cạnh của nó tăng thêm 20%?
Bài giải:
Gọi độ dài một cạnh của hình vuông là a. (Điều kiện: a > 0)
Độ dài cạnh hình vuông lúc sau là: .
Từ đó, ta có:
Vậy diện tích hình vuông đã tăng thêm 44%.
Ví dụ 2: Cho hình chữ nhật có chu vi 320 cm, diện tích . Tính chiều dài và chiều rộng của hình chữ nhật đó.
Bài giải:
Gọi độ dài của chiều dài và chiều rộng của hình chữ nhật đã cho lần lượt là a và b. (Điều kiện a, b > 0)
Theo đề bài ta có:
Giải ra, ta được: a = 100 và b = 60.
 BÀI TẬP VẬN DỤNG
BÀI TẬP VẬN DỤNG
 BÀI TẬP CƠ BẢN
BÀI TẬP CƠ BẢN
Bài 1: Tính diện tích một tam giác vuông có cạnh huyền bằng 13cm và tổng hai cạnh góc vuông bằng 17cm.
Bài giải:
Gọi độ dài của hai cạnh góc vuông lần lượt là x và y.(Điều kiện: x, y > 0)
Theo đề bài ta có:
Từ đó tính được hoặc
.
Diện tích tam giác đó là: .
Bài 2: Cho hình chữ nhật ABCD, E là điểm tùy ý trên cạnh AB. Chứng minh .
Bài giải:
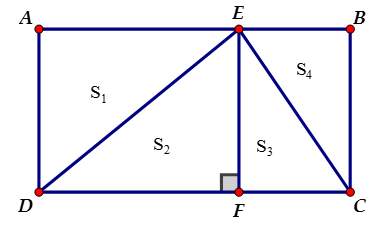
Kẻ ta có
Tương tự
Gọi lần lượt là diện tích các tam giác (theo hình vẽ), ta có:
hay .
 BÀI TẬP NÂNG CAO
BÀI TẬP NÂNG CAO
Bài 1: Cho hình chữ nhật ABCD có AB = 6cm; AC = 10 cm. Gọi O là giao điểm hai đường chéo AC và BD và M, N, P, Q lần lượt là trung điểm của OA, OB, OC, OD.
Bài giải:
a) Tính .
b) Chứng minh rằng .
Bài giải:
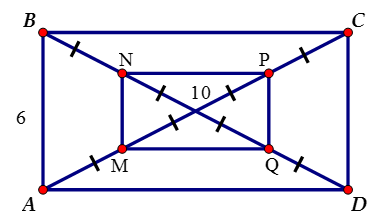

a) Ta có MN và PQ lần lượt là các đường trung bình của các tam giác AOB và COD mà
Tương tự
Do đó MNPQ là hình chữ nhật.
Trong
nên
Vậy
b) Dễ thấy
Do đó
Bài 2: Trong các hình chữ nhật có cùng diện tích bằng 100m2, hình nào có chu vi nhỏ nhất?
Bài giải:
Gọi độ dài của chiều dài và chiều rộng của hình chữ nhật lần lượt là a và b.
(Điều kiện: a, b >0)
Bài toán được diễn đạt lại là: “Cho a, b > 0 và a.b = 100. Tìm giá trị nhỏ nhất của biểu thức 2(a+b)”.
Áp dụng bất đẳng thức Cô-si cho 2 số dương a và b, ta thu được chu vi nhỏ nhất bằng 40cm khi a = b = 10cm hay hình chữ nhật trở thành hình vuông.
Chúc các em học tập hiệu quả!

