Trang chủ
LỚP 9 Toán cơ bản Ôn bài lý thuyết CHƯƠNG VI. ĐƯỜNG TRÒN 6.1. Sự xác định của đường tròn. Tính chất đối xứng của đường tròn
6.1. Sự xác định của đường tròn. Tính chất đối xứng của đường tròn
Nội dung chính
ÔN TẬP: SỰ XÁC ĐỊNH CỦA ĐƯỜNG TRÒN. TÍNH CHẤT ĐỐI XỨNG CỦA ĐƯỜNG TRÒN.
![]() KIẾN THỨC CẦN NHỚ
KIẾN THỨC CẦN NHỚ
1. Định nghĩa
Đường tròn tâm O có bán kính R là hình gồm các điểm cách điểm O một khoảng bằng R, trong đó R > 0. Kí hiệu (O; R) hoặc (O).
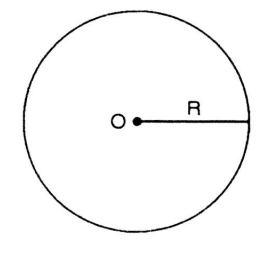
2. Cách xác định đường tròn
a) Định lí: Qua ba điểm không thẳng hàng bao giờ cũng vẽ được một và chỉ một đường tròn.
Đường tròn đi qua ba đỉnh A, B, C của ΔABC là đường tròn ngoại tiếp tam giác ABC.
Khi đó ΔABC gọi là tam giác nội tiếp đường tròn.
b) Các cách xác định một đường tròn.
– Cách 1: Một điểm O cho trước và một số thực dương R cho trước, ta xác định được duy nhất một đường tròn tâm O bán kính R.
– Cách 2: Ba điểm không thẳng hàng, ta xác định được duy nhất một đường tròn đi qua ba điểm đó.
3. Tâm đối xứng – Trục đối xứng
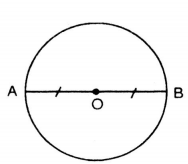
a) Tâm đối xứng
Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.
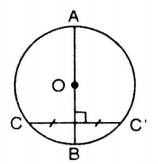
b) Trục đối xứng
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn.
 BÀI TẬP VÍ DỤ
BÀI TẬP VÍ DỤ
Ví dụ 1: Cho tam giác đều ABC. Gọi M, P và S lần lượt là trung điểm cả ba cạnh AB, BC và AC.
Chứng minh rằng bốn điểm B, M, S và C cùng nằm trên một đường tròn có tâm là P.
Bài giải:
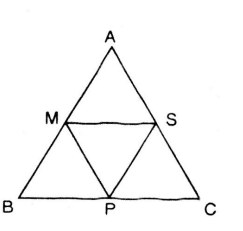
Nối và
Vì
Do đó:
Vì
Từ (1) và (2) ta có:
Vậy bốn điểm




Bài 1:
Bài 2:


Bài 1:
Bài 2:
Xem thêm: Đường kính và dây của đường tròn
Trên đây là các kiến thức cần nhớ và các bài tập ví dụ minh họa về nội dung của bài học Sự xác định của đường tròn. Tính chất đối xứng của đường tròn – toán cơ bản lớp 9.
Chúc các em học tập hiệu quả!

