7.6. Tính chất ba đường phân giác của tam giác

Hướng dẫn giải bài tập sgk toán lớp 7 tập 2 trang 72, 73. Bài học Tính chất ba đường phân giác của tam giác.

Bài 36. (Trang 72 SGK Toán 7 – Tập 2)

Cho tam giác DEF, điểm I nằm trong tam giác và cách đều ba cạnh của nó.

Chứng minh I là điểm chung của ba đường phân giác của tam giác DEF.

Bài giải

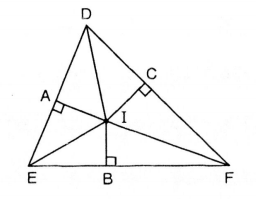
Từ điểm I, ta kẻ

– Vì điểm I cách đều hai cạnh DE và DF nên điểm I nằm trên đường phân giác của .

– Tương tự, vì điểm I cách đều hai cạnh ED và EF nên điểm I nằm trên đường phân giác của .

– Vì điểm I cách đều hai cạnh FE và FD nên điểm I nằm trên đường phân giác của

Vậy I là điểm chung của ba đường phân giác của (đpcm)

 

Bài 37. (Trang 72 SGK Toán 7 – Tập 2)

Nêu cách vẽ điểm K ở trong tam giác MNP mà các khoảng cách từ K đến ba cạnh của tam giác đó bằng nhau. Vẽ hình minh họa.

Bài giải

a) Cách vẽ: – Dựng tia phân giác MJ của góc M.

– Dựng tia phân giác NQ của góc N.

Vậy K là giao điểm của MJ và NQ, đó là điểm cần dựng.

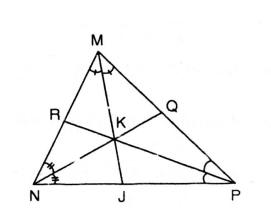
b) Chứng minh: Vì K là giao điểm của hai đường phân giác MJ và NQ xuất phát từ điểm M và N của tam giác MNP.

Theo định lí 2 về tính chất ba tia phân giác của tam giác thì điểm K cách đều ba cạnh của tam giác MNP.

Vậy điểm I dựng được thỏa mãn yêu cầu bài toán.

 

Bài 38. (Trang 73 SGK Toán 7 – Tập 2)

Cho hình dưới:

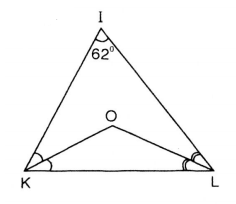
a) Tính góc KOL.

b) Kẻ tia IO, hãy tính góc KIO.

c) Điểm O có cách đều ba cạnh của tam giác IKL hay không? Tại sao?

Bài giải

a) Trong tam giác KOL, ta có:

Trong tam giác IKL, ta có:

Thế vào (1) ta được:

Vậy

b) Theo hình vẽ ta có KO là đường phân giác của và LO là đường phân giác của . Nối IO sẽ là đường phân giác của góc I (vì 3 đường phân giác trong tam giác cũng đi qua một điểm)

Vậy .

c) Vì O là giao điểm của ba đường phân giác của . Do đó, điểm O cách đều ba cạnh của .

Bài 39. (Trang 73 SGK Toán 7 – Tập 2)

Cho hình bên:

a) Chứng minh:

b) So sánh góc DBC và góc DCB.

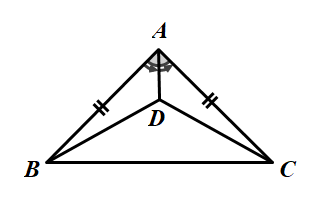
Bài giải

a) Chứng minh

Xét hai tam giác ABD và ACD, ta có:

AD: cạnh chung.

Vậy

b) Vì

Hơn nữa, cân ở A (vì AB = AC)

Từ (1) và (2), ta có:

Vậy .

Bài 40. (Trang 73 SGK Toán 7 – Tập 2)

Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng.

Bài giải

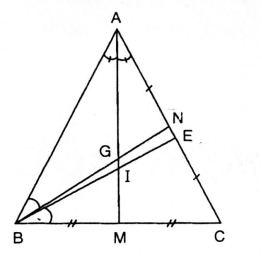
Vì cân tại A và AM, BN là 2 đường trung tuyến chúng cắt nhau tại G.

Vậy G thuộc AM   (1)

Vì I là điểm nằm trong tam giác ABC và cách đều ba cạnh nên I là giao điểm ba đường phân giác trong.

Ta có: cân tại A nên đường thẳng AM là đường trung tuyến cũng là đường phân giác nên I thuộc AM   (2)

Từ (1) và (2) suy ra: Ba điểm A, G, I thẳng hàng, hay trong tam giác cân ABC (AB= AC) đỉnh A, điểm cách đều ba cạnh và trọng tâm của tam giác là ba điểm thằng hàng.

Bài 41. (Trang 73 SGK Toán 7 – Tập 2)

Hỏi trọng tâm của một tam giác đều có cách đều ba cạnh của nó hay không? Vì sao?

Bài giải

Trả lời: Trong tam giác đều, ba đường trung tuyến đồng thời là ba đường phân giác, do đó trọng tâm G (giao điểm của ba đường trung tuyến) cũng là điểm cách đều (giao điểm ba đường phân giác) ba cạnh của tam giác.

Bài 42. (Trang 73 SGK Toán 7 – Tập 2)

Chứng minh định lý: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân.

Gợi ý: Trong , nếu AD vừa là đường trung tuyến vừa là đường phân giác thì kéo dài trung tuyến AD một đoạn sao cho . Chứng minh , suy ra . Sau đó chứng minh tam giác cân, suy ra . Từ đó suy ra được tam giác ABC cân.

Bài giải

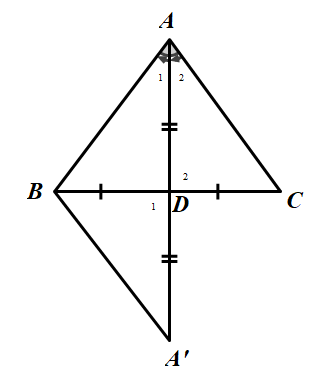
Kéo dài trung tuyến AD một đoạn sao cho

– Xét hai tam giác ADC và ADB, ta có:

BD = DC (do AD là trung tuyến)

(đối đỉnh)

(do cách vẽ)

Vậy

Suy ra

Mà

– Xét tam giác , ta có:

Vậy tam giác BAD cân tại B, nên

Từ (1) và (2) ta được:

Vậy là tam giác cân tại A (đpcm)

Bài 43. (Trang 73 SGK Toán 7 – Tập 2)

Đố: Có hai con đường cắt nhau và cùng cắt một con sông tại hai điểm khác nhau (hình vẽ).

Hãy tìm một điểm để xây dựng một đài quan sát sao cho các khoảng cách từ đó đến hai con đường và đến bờ song bằng nhau.

Có tất cả mấy điểm như vậy?

 

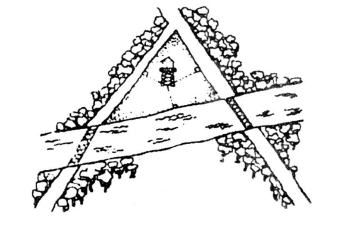
Bài giải

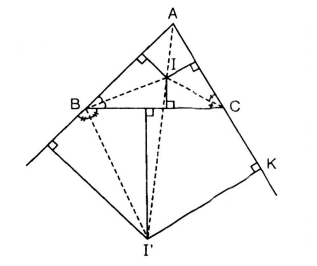
Hướng dẫn: Ta hình dung hai con đường cắt nhau và cùng cắt một con sông tạo thành tam giác ABC.

Địa điểm để xây dựng đài quan sát thỏa mãn yêu cầu đề bài phải là giao điểm 3 đường phân giác trong cảu tam giác ABC.

Hơn nữa giao điểm của hai đường phân giác ngoài của góc và cũng thỏa mãn điều kiện của đề bài (xem lại bài tập 31).

Vậy các địa điểm để xây dựng đài quan sát là I, I’

Xem thêm Hướng dẫn giải bài tập sgk toán 7 Tính chất đường trung trực của đoạn thẳng.