7.10. Ôn tập chương VII

Hướng dẫn giải bài tập sgk toán lớp 7 tập 2 trang 87, 88. Bài học Ôn tập chương VII.

Bài 63. (Trang 87 SGK Toán 7 – Tập 2)

Cho tam giác ABC với AC < AB. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Vẽ các đoạn thẳng AD, AE.

a) Hãy so sánh góc ADC và góc AEB.

b) Hãy so sánh các đoạn thẳng AD và AE.

Bài giải

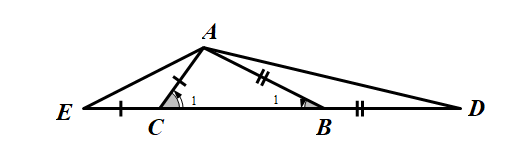
a) Trong , ta có:

Từ (1) suy ra được: (hai góc kề bù)  (2)

– Trong tam giác cân ACE, ta có:

và

hay

– Tương tự, trong tam giác cân ABD, ta có:

– Mà (do (2))

Từ (2), (3) và (4) suy ra

hay hay (đpcm)

b) Xét , ta có: . Suy ra AD > AE.

 

Bài 64. (Trang 87 SGK Toán 7 – Tập 2)

Gọi MH là đường cao của tam giác MNP.

Chứng minh rằng: Nếu MN < MP, thì HN < HP và

(Yêu cầu xét hai trường hợp: Khi góc N nhọn và khi góc N tù)

Bài giải

Trường hợp là góc nhọn.

Ta có MN, MP, MH là các đường xiên và đường vuông góc kẻ từ điểm M đến đường thẳng NP.

Theo giả thiết, ta có MN < MP và NH, HP lần lượt là hình chiếu của MN, MP lên NP.

Vậy HN < HP (định lý đảo)

Chứng minh

vuông tại H nên

vuông tại H nên

Trong , vì MN < MP

Từ (1), (2) và (3) ta suy ra được:

hay (đpcm)

* Trường hợp góc N là góc tù: (Học sinh chứng minh tương tự).

 

Bài 65. (Trang 87 SGK Toán 7 – Tập 2)

Có thể vẽ được mấy tam giác (phân biệt) với ba cạnh là ba trong năm đoạn thẳng có độ dài như sau: 1cm; 2cm; 3cn; 4cm và 5cm?

Bài giải

Về lí thuyết trong năm số 1, 2, 3, 4, 5 thì ta có thể chọn ra bộ 3 số để vẽ tam giác có độ dài 3 cạnh tương ứng với bộ 3 số đó.

Trong năm số 1, 2, 3, 4, 5 ta có bộ ba số như sau:

Mà ta biết rằng trong một tam giác độ dài mỗi cạnh bao giờ cũng nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài hai cạnh còn lại. Do đó ta chỉ vẽ được ba tam giác (phân biệt) có độ dài 3 cajh lần lượt là: và

Bài 66. (Trang 87 SGK Toán 7 – Tập 2)

Đố: Bốn điểm dân cư được xây dựng như hình dưới. Hãy tìm vị trí đặt một nhà máy sao cho tổng các khoảng cách từ nhày máy đến bốn khu dân cư này là nhỏ nhất.

 

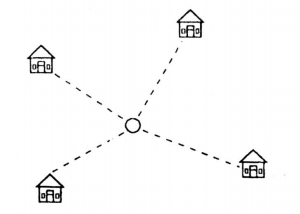
Bài giải

Gọi O là nơi phải đặt nhà máy. A, B, C, D lần lượt là bốn điểm dân cư.

Tổng khoảng cách từ nhà máy đến 4 khu đân cư là: OA + OB + OC + OD.

Ta có:

+ Nếu O nằm trên đoạn AC (và O không trùng với giao điểm của AC và BD) thì

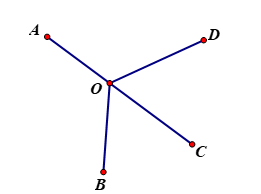
+ Nếu O trùng với M nằm trên đoạn BD (và O không trùng với giao điểm của AC và BD) hình vẽ dưới thì

+ Nếu O (trùng với M) không nằm trên đoạn AC và BD (hình vẽ dưới) thì theo bất đẳng thức tam giác, ta có:

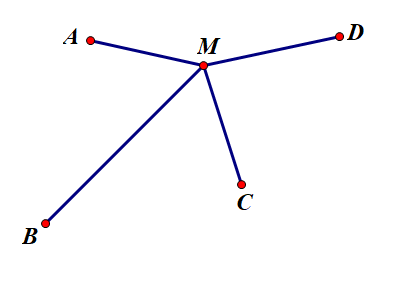
+ Nếu O là giao điểm của AC và BD thì

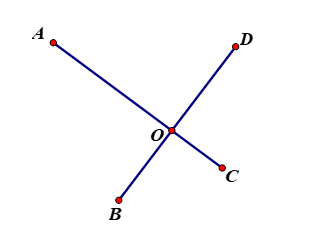
Vậy khi O là giao điểm của AC và BD thì tổng khoảng cách từ nhà máy này đến các khu dân cư ngắn nhất.

 

Bài 67. (Trang 87 SGK Toán 7 – Tập 2)

Cho tam giác MNP với trung tuyến MR và trọng tâm Q.

a) Tính tỉ số các diện tích của hai tam giác MPQ và RPQ.

b) Tính tỉ số các diện tích của hai tam giác MNP và RNQ.

c) So sánh các diện tích của hai tam giác RQP và RNQ.

Từ các kết quả trên, hãy chứng minh các tam giác QMN, QNP, QPM có cùng diện tích.

Gợi ý: Hai tam giác ở mỗi câu a, b, c có chung đường cao.

Bài giải

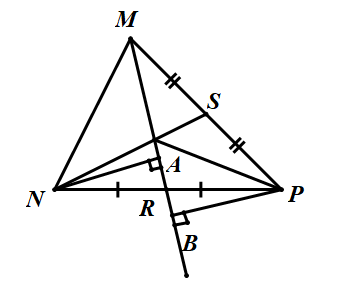
a) Vẽ 

Vậy tam giác MPQ và RPQ có chung đường bao PB.

Vì Q là trọng tâm của nên MQ = 2QR

Ta có:

và

Vậy

b) Vẽ

Vậy NA là đường cao của đồng thời là đường cao của .

Vì Q là trọng tâm của nên MQ = 2QR.

Ta có:

và

Vậy

c) Xét hai tam giác vuông ANR và BPR, ta có:

Ta có:

Vậy

* Từ kết quả câu a) ta có:

(do câu c)

* Từ kết quả câu b), ta có:

Từ và suy ra:

(đpcm)

Bài 68. (Trang 88 SGK Toán 7 – Tập 2)

Cho góc xOy. Hai điểm A, B lần lượt nằm trên hai cạnh Ox, Oy.

a) Hãy tìm điểm M cách đều hai cạnh của góc xOy và cách đều hai điểm A, B.

b) Nếu OA = OB thì có bao nhiêu điểm M thỏa mãn các điều kiện trong câu a?

Bài giải

a)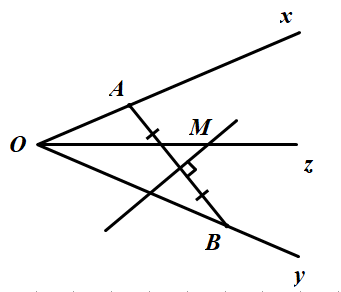

Tìm M khi

– Vì M cách đều hai cạnh Ox, Oy của nên M nằm trên đường phân giác Oz của góc xOy  (1)

– Vì M cách đều hai điểm A, B nên M nằm trên đường trung trực của đoạn AB  (2).

Từ (1) và (2) ta xác định được điểm M là giao điểm của đường phân giác Oz của và đường trung trực của đoạn AB.

b)

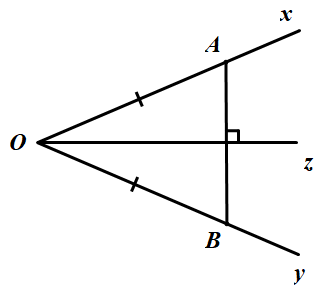
Tìm M khi OA = OB

– Vì điểm M cách đều hai cạnh của góc xOy nên M nằm trên đường phân giác của góc xOy  (3)

– Ta có OA = OB. Vậy cân tại O. Trong tam giác cân OAB đường phân giác Oz cũng là đường trung trực của đoạn AB  (4)

Từ (3) và (4) ta xác định được vô số điểm M nằm trên Oz thỏa mãn điều kiện đề bài.

Bài 69. (Trang 88 SGK Toán 7 – Tập 2)

Cho hai đường thẳng phân biệt không song song, không vuông góc a và b, điểm M không nằm trên hai đường thẳng này. Qua M lần lượt vẽ đường thẳng c vuông góc với a tại P, cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S. Chứng minh rằng đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b.

Bài giải

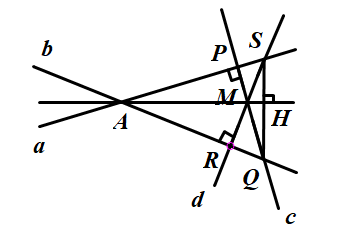
Vì hai đường thẳng a và b không song song nên a và b cắt nhau tại điểm A.

– Xét , ta có:

và

Ta có QP và RS cắt nhau tại M.

Vậy M là trực tâm của

– Đường thẳng đi qua trực tâm M và vuông góc với QS tại H sẽ là đường cao thứ ba của

Vậy MH phải đi qua đỉnh A của hay đường thẳng vuông góc với QS đi qua giao điểm của hai đường thẳng a và b (đpcm)

Bài 70. (Trang 88 SGK Toán 7 – Tập 2)

Cho A, B là hai điểm phân biệt và d là đường trung trực của đoạn thẳng AB.

a) Ta kí hiệu là nửa mặt phẳng bờ d có chứa điểm A (không kể đường thẳng d). Gọi N là một điểm của và M là giao điểm của đường thẳng NB và d. Hãy so sánh NB với NM + MA; từ đó suy ra NA < NB.

b) Ta kí hiệu là nửa mặt phẳng bờ d có chứa điểm B (không kể d). Gọi N’ là một điểm của . Chứng minh rằng

c) Gọi L là một điểm sao cho LA < LB. Gọi điểm L nằm ở đâu, trong , hay trên d?

Bài giải

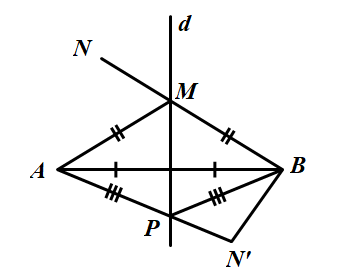
a) So sánh NB với NM + MA.

* Ta có M nằm trên đường trung trực của AB nên MA = MB.

Vì M nằm giữa đoạn NB nên: NB = NM + MB

hay NM = NM + MA (vì MB = MA)

Vậy NB = NM + MA

* Vì MA + NM = NB (trong đó NM > 0)

Suy ra MA < NB (đpcm)

b) Chứng minh NA < NA.

Tương tự chứng minh câu a)

Trong nửa mặt phẳng ta lấy điểm . Nối cắt d tại P.

Vì P nằm trên đường trung trực của đoạn AB nên: PA = PB.

Ta có:

Trong ta có:

Do đó: (đpcm)

c) Theo chứng minh ở câu a) muốn cho LA < LB thì điểm L phải nằm trên

Xem thêm Hướng dẫn giải bài tập sgk toán 8 Tứ giác