7.4. Tính chất ba đường trung tuyến của tam giác
Hướng dẫn giải bài tập sgk toán lớp 7 tập 2 trang 66, 67. Bài học Tính chất ba đường trung tuyến của tam giác.
Nội dung chính
Bài 23. (Trang 66 SGK Toán 7 – Tập 2)
Cho G là trọng tâm của tam giác DEF với đường trung tuyến DH ( hình bên)
Trong các khẳng định sau đây, khẳng định nào đúng?
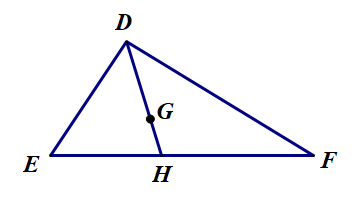
Bài giải
Khẳng định là khẳng định đúng. Các khẳng định còn lại đều sai.
Bài 24. (Trang 66 SGK Toán 7 – Tập 2)
Cho hình bên. Hãy điền số thích hợp vào chỗ trống trong các đẳng thức sau:
a)
b) ;
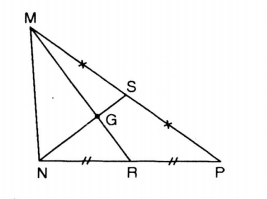
Bài giải
a)
b)
Bài 25. (Trang 67 SGK Toán 7 – Tập 2)
Biết rằng: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền. Hãy giải bài toán sau:
Cho tam giác vuông ABC có hai cạnh góc vuông AB = 3cm; AC = 4cm. Tính khoảng cách từ đỉnh A tới trọng tâm G của tam giác ABC.
Bài giải
Áp dụng định lý Py-ta-go trong tam giác vuông ABC, ta có:
(cm)
Mà (cm)
Ta có (cm).
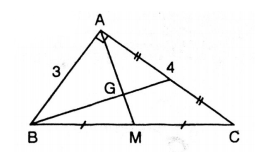
Bài 26. (Trang 67 SGK Toán 7 – Tập 2)
Chứng minh định lí: Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.
Bài giải
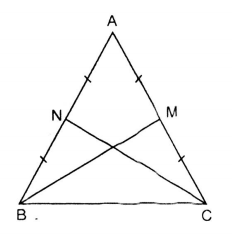
– Vì cân tại A nên:
– Xét hai tam giác NBC và MBC, ta có:
BC: cạnh chung
Vậy
Suy ra NC = MB (đpcm)
Bài 27. (Trang 67 SGK Toán 7 – Tập 2)
Hãy chứng minh định lí đảo của định lí trên: Nếu tam giác có hai đường trung tuyến bằng nhau thì đó là tam giác cân.
Bài giải
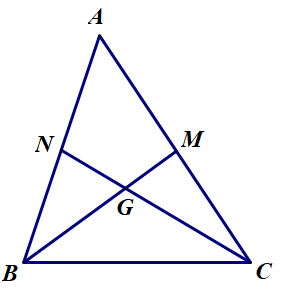

Gọi G là giao điểm của hai đường trung tuyến BM và CN. Do đó G là trọng tâm của
– Ta có:
Ta có:
Xét hai tam giác BGN và CGM, ta có:
Vậy
Bài 28. (Trang 67 SGK Toán 7 – Tập 2)
Cho tam giác DEF cân tại D với trung tuyến DI.
a) Chứng minh
b) Các góc DIE và góc DIF là những góc gì?
c) Biết DE = DF = 13cm; EF = 10cm, hãy tính độ dài đường trung tuyến DI.
Bài giải
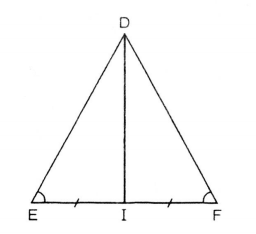

a) Vì DI là trung tuyến nên IE = IF
Xét hai tam giác DEI và DFI, ta có:
Vậy
b) Vì
Hơn nữa
hay
Vậy
c) Theo chứng minh ở câu b) tam giác DEI vuông ở I có:
Áp dụng định lý Py-ta-go trong tam giác vuông DEI, ta có:
Bài 29. (Trang 67 SGK Toán 7 – Tập 2)
Cho G là trọng tâm của tam giác đều ABC. Chứng minh rằng: GA = GB = GC.
Hướng dẫn: Áp dụng định lí ở bài tập 26.
Bài giải
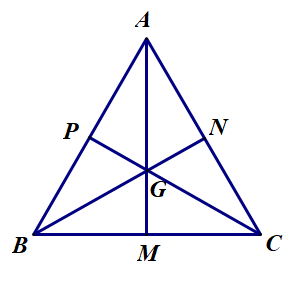

Vì
– Xét
và
– Xét
Vậy
Và
Từ (1) và (2) ta suy ra:
Bài 30. (Trang 67 SGK Toán 7 – Tập 2)
Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G’ sao cho G là trung điểm AG’.
a) So sánh các cạnh của tam giác ABC. Trên tia AG lấy điểm G’ sao cho G là trung điểm của AG’.
b) So sánh các đường trung tuyến của tam giác BGG’ với các cạnh của tam giác ABC.
Bài giải
a) So sánh các cạnh của
Gọi M, N, E lần lượt là trung điểm của BC, CA, AB.
G là trọng tâm của tam giác ABC
Mà
– Vì G là trọng tâm của
– Ta có:
Xét
GM = MG’ (chứng minh trên)
MB = MC (M là trung điểm BC)
Vậy
Mà
Vậy
Hay mỗi cạnh của
b) So sánh các đường trung tuyến của
– Ta có: BM là đường trung tuyến
Mà M là trung điểm của BC nên
Gọi I là trung điểm BG
Vì
Xét
IG = GN (chứng minh trên)
GG’ = GA (giả thiết)
Vậy
– Gọi K là trung điểm
Vì
Mà K là trung điểm
Vì
Xét
EG = KG’ (chứng minh trên)
AG = GG’ (giả thiết)
Vậy
Mà
Vậy
Hay mỗi đường trung tuyến của tam giác BGG’ bằng một nửa cạnh của tam giác ABC.
Xem thêm Hướng dẫn giải bài tập sgk toán 7 Tính chất tia phân giác của một góc.

