7.9. Tính chất ba đường cao của tam giác
Hướng dẫn giải bài tập sgk toán lớp 7 tập 2 trang 83. Bài học Tính chất ba đường cao của tam giác.
Nội dung chính
Bài 58. (Trang 83 SGK Toán 7 – Tập 2)
Hãy giải thích tại sao trực tâm của tam giác vuông trùng với đỉnh góc vuông và trực tâm của tam giác tù nằm ở bên ngoài tam giác.
Bài giải
* Trực tâm của tam giác vuông trùng với đỉnh góc vuông.
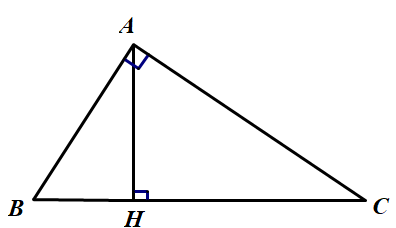
Cho tam giác ABC vuông tại A.
– Vẽ đường cao AH ứng với cạnh BC.
– Đường cao xuất phát từ đỉnh B ứng với cạnh AC chính là BA.
– Đường cao xuất phát từ đỉnh C ứng với cạnh AB chính là CA.
Ba đường cao này cắt nhau tại A. Vậy A là trực tâm của tam giác vuông ABC. Hay trực tâm của tam giác vuông trùng với đỉnh góc vuông.
* Trực tâm của tam giác tù nằm ở bên ngoài tam giác.
Cho tam giác ABC tù ( 
)
– Vẽ đường cao AN ứng với cạnh BC.
– Vẽ đường cao xuất phát từ đỉnh B ứng với cạnh AC, đó là đường BK (nằm ngoài 
)
– Vẽ đường cao xuất phát từ đỉnh C ứng với cạnh AB, đó là đường CP (nằm ngoài )
Ba đường cao AN, BK, CP cắt nhau tại H (ngoài ngoài )
Vậy H là trực tâm của .
Trực tâm của một tam giác tù nằm ngoài tam giác vì trong một tam giác tù, hai đường cao xuất phát từ hai góc nhọn nằm ngoài tam giác. Khi đó ba đường cao sẽ cắt nhau tại một điểm nằm ngoài tam giác đó.
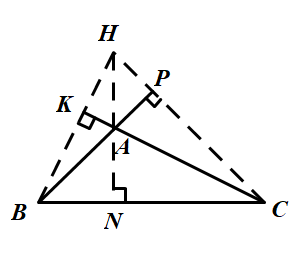
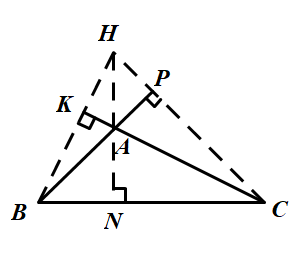
Bài 59. (Trang 83 SGK Toán 7 – Tập 2)
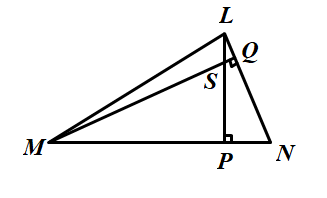
Cho hình bên.
a) Chứng minh 
b) Khi 
, hãy tính góc MSP và góc PSQ.
Bài giải
a) Chứng minh 
Trong tam giác LMN, ta có:
và LP cắt MQ tại S.
Vậy S là trực tâm của tam giác LMN. Suy ra NS là đường cao thứ ba của tam giác LMN hay 
(đpcm)
b) * Tính 
– Trong tam giác vuông QMN ta có:
hay 
– Trong tam giác vuông SMP, ta có:
hay 
Vậy 
* Tính 
Ta có: 
hay 
Vậy 
Bài 60. (Trang 83 SGK Toán 7 – Tập 2)
Trên đường thẳng d, lấy ba điểm phân biệt I, J, K (J ở giữa I và K)
Kẻ đường thẳng 
vuông với với d tại J. Trên lấy điểm M khác với điểm J. Đường thẳng qua I vuông góc với MK cắt tại N.
Chứng minh rằng 
Bài giải
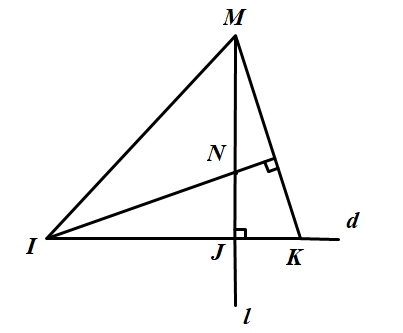
Chứng minh
Nối M với I và M với K ta được tam giác MIK.
Trong 
, ta có:
(do 
(do đường thẳng đi qua I vuông góc với MK) và MJ cắt IN tại N.
Vậy N là trực tâm của tam giác
Suy ra KN là đường cao thứ ba của hay 
(đpcm)
Bài 61. (Trang 83 SGK Toán 7 – Tập 2)
Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.
b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB và HAC.
Bài giải
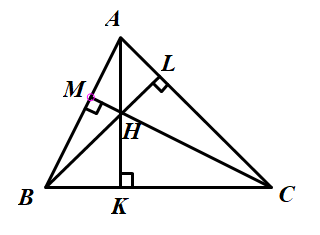
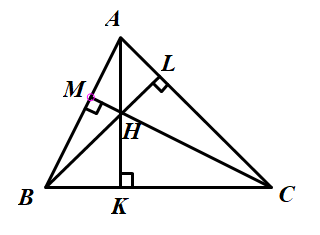
a) Vì H là trực tâm của nên: 
.
– Trong 
ta có: 
(do 
)
– Từ B vẽ đường cao ứng với cạnh CH của , ta được BM trùng với cạnh AB của .
– Tương tự, từ C vẽ đường cao ứng với cạnh BH của , ta được CL trùng với cạnh AC của .
Ba đường cao HK, BM và CL cắt nhau tại A. Vậy A là trực tâm của tam giác HBC.
b) Tương tự câu a), C là trực tâm của 
, B là trực tâm của 
.
Bài 62. (Trang 83 SGK Toán 7 – Tập 2)
Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó chứng minh một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
Bài giải
a)
Vẽ 
và 
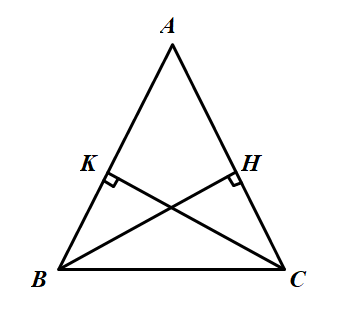
– Xét hai tam giác vuông KBC và HCB, ta có:
BC: cạnh chung
BH = CK (gt)
Vậy 
– Xét tam giác ABC, ta có:
hay 
Vậy 
cân tại A (đpcm)
b)
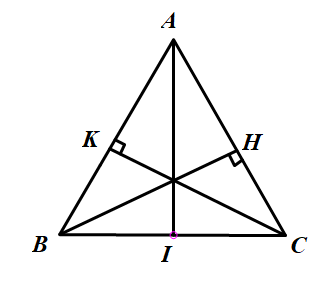
Theo câu a)
– Nếu BH = CK thì cân tại A 
– Nếu AI = BH thì cân tại C 
Từ (1) và (2) ta có: AB = BC = AC.
Vậy là tam giác đều.
Xem thêm Hướng dẫn giải bài tập sgk toán 7 Ôn tập chương VII
Bạn có thể in hoặc xuất file pdf! Thật tuyệt!
