Bài 7: Bài tập về hình tam giác

PHẦN I: ĐỀ BÀI

Bài 1: Cho tam giác ABC vuông tại A, có cạnh AB = 24cm, cạnh AC = 32cm. Điểm M nằm trên cạnh AC. Từ M kẻ đường song song với cạnh AB cắt BC tại N. Đoạn MN dài 16cm. Khi đó độ dài đoạn AM bằng bao nhiêu ?

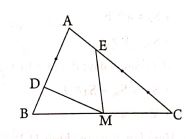
Bài 2: Cho tam giác ABC có diện tích bằng .

Biết DA = 2DB; EC = 3EA; MC = MB (hình vẽ).

Tính tổng diện tích hai tam giác MDB và MCE.

Bài 3: Tam giác ABC có diện tích bằng , cạnh AB dài 40cm, cạnh AC dài 24cm, chiều cao AH dài 20cm. Khi đó chu vi tam giác ABC bằng bao nhiêu ?

Bài 4: Người ta cắt một hình tam giác bằng gỗ, có chiều cao bằng số đo cạnh tương ứng, biết tổng số đo của cạnh đáy và chiều cao bằng 30dm. Hỏi hình tam giác đó có diện tích bằng bao nhiêu ?

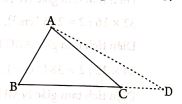
Bài 5: Một miếng đất hình tam giác có cạnh đáy bằng 32m, người ta mở rộng miếng đất ấy bằng cách kéo dài cạnh đáy thêm 4m thì được một miếng đất mới cũng có hình tam giác và diện tích sau hơn diện tích ban đầu là . Tính diện tích miếng đất lúc chưa mở rộng.

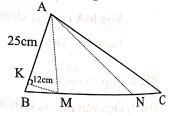
Bài 6: Cho tam giác ABC có cạnh AB dài 25cm, trên cạnh BC lấy hai điểm M, N sao cho độ dài đoạn BM bằng  độ dài đoạn BC, độ dài đoạn CN bằng độ dài đoạn BC, biết chiều cao kẻ từ M của tam giác AMB là 12cm. Tìm diện tích tam giác ANC và diện tích tam giác AMN.

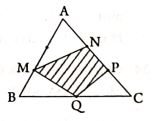
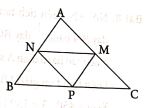
Bài 7: Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm của các cạnh CA, AB, BC. Nối MO, MN, NP. Khi đó hãy chứng tỏ:

a)

b) Đoạn MN song song với cạnh BC và bằng một nửa cạnh BC.

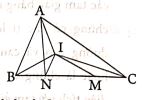
Bài 8: Cho tam giác ABC có diện tích bằng . M và N là hai điểm trên cạnh BC và các đoạn CM, MN< NB dài bằng nhau. Từ M kẻ đường thẳng song song với cạnh AC. Từ N kẻ đường thẳng song song với cạnh AB, chúng cắt nhau tại I. Nối IA, IB, IC. Tính diện tích các tam giác IAC, IAB, IBC.

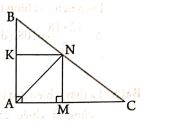
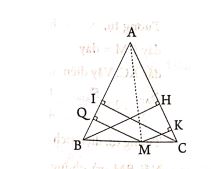
Bài 9: Cho tam giác cân ABC (AB = AC). Từ B và C kẻ đường cao BH đến AC, CI đến AB

a) So sánh độ dài BH và CI

b) Cho M là điểm bất kì trên cạnh BC (M ở giữa B và C). Từ M kẻ các đường vuông góc MQ đến AB và MK đến AC. Cho biết BH = 25cm. Tính độ dài MQ + MK

Bài 10: Chọn đáp án đúng:

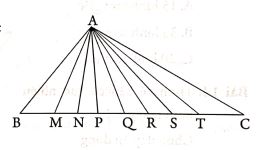
Có bao nhiêu hình tam giác đỉnh A ?

A. 8 hình tam giác

B. 9 hình tam giác

C. 36 hình tam giác

D. 18 hình tam giác

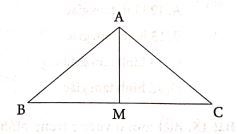
Bài 11: Cho hình vẽ bên có BM = MC. So sánh diện tích tam giác ABM với diện tích tam giác ABC.

Chọn đáp án đúng:

A. Diện tích tam giác ABM bằng một nửa diện tích tam giác ABC.

B. Diện tích tam giác ABM bằng một phần ba diện tích tam giác ABC.

C. Diện tích tam giác ABM bằng một phần tư diện tích tam giác ABC.

Bài 12: Chọn đáp án đúng:

a) Trong hình vẽ có bao nhiêu đoạn thẳng ?

A. 12 đoạn thẳng

B. 13 đoạn thẳng

C. 14 đoạn thẳng

D. 15 đoạn thẳng

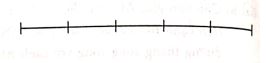
b) Trong hình vẽ có bao nhiêu tam giác ?

A. 7 hình tam giác

B. 8 hình tam giác

C. 9 hình tam giác

D. 10 hình tam giác

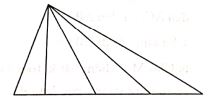
Bài 13: Em hãy đếm số hình tam giác ở hình vẽ. Chọn đáp án đúng:

A. 15 hình tam giác

B. 35 hình tam giác

C. 20 hình tam giác

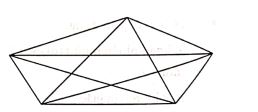
Bài 14: Hình vẽ bên có bao nhiêu hình tam giác ?

Chọn đáp án đúng:

A. 12 hình tam giác

B. 13 hình tam giác

C. 14 hình tam giác

D. 15 hình tam giác

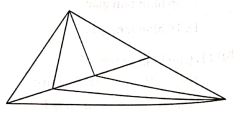
Bài 15: Biết mỗi ô vuông trong hình dưới đây đều có diện tích là . Hãy tính diện tích hình tam giác PQR.

Chọn đáp án đúng:

A.

B.

C.

D.

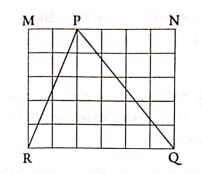
Bài 16: Cho tam giác có diện tích là . Biết AB = 3BM; AN = NP = PC; QB = QC (như hình vẽ bên). Tính diện tích tứ giác MNPQ.

PHẦN II: BÀI GIẢI

Bài 1:

Nối AN ta có tam giác ACN có NM là chiều cao, vì MN song song với AB nên MN cũng vuông góc với AC.

Diện tích tam giác ACN là:

Diện tích tam giác ABC là:

Diện tích tam giác NAB là:

Chiều cao NK hạ từ N xuống AB có số đo là:

Vì MN song song với AB nên tứ giác MNBA là hình thang vuông. Vậy MA cũng là chiều cao của hình thang MNBA. Do đó MA cũng bằng cm.

Bài 2: Đáp số:

Bài 3: Dựa vào các dữ kiện đề bài, cùng với các chú ý về các công thức cần nhớ, ta có thể tính được như sau:

Số đo cạnh BC là:

Từ đó, ta có chu vi tam giác ABC là:

Đáp số: 114cm

Bài 4: Theo đề bài ta có:

Tổng số phần bằng nhau: 2 + 3 = 5 (phần)

Chiều cao của hình tam giác bằng: (30 : 5) x 2 = 12 (dm)

Cạnh đáy của hình tam giác bằng: 30 – 12 = 18 (dm)

Diện tích của hình tam giác bằng:

Đáp số:

Bài 5: Ta thấy, chiều cao của tam giác ACD cũng là chiều cao của tam giác ABC  có độ dài bằng:

 

Từ đó, ta tính được diện tích mảnh đất lúc chưa mở rộng có diện tích bằng:

Đáp số:

Bài 6: Từ hình vẽ bên, ta nhận thấy, diện tích tam giác ABC bằng tổng ba diện tích hình tam giác ABM, AMN và ANC. Diện tích tam giác ABM bằng:

Nhận xét: Ba tam giác ABM, AMN, ANC có cùng chiều cao kẻ từ A. Từ đó, dựa vào điều kiện đề bài, có thể coi cạnh BC được chia thành 6 phần bằng nhau, thì BM chiếm 2 phần, NC chiếm 1 phần và MN chiếm 3 phần. Từ đó, đoạn MN bằng đoạn BM.

Vậy diện tích tam giác AMN bằng diện tích tam giác ABM và bằng

Ta có, đoạn NC bằng đoạn MN nên diện tích tam giác ANC bằng diện tích tam giacsAMN và bằng:

Đáp số:

Bài 7: Để chứng minh được diện tích của các tam giác bằng nhau, ta cần chỉ ra chúng có các tỉ lệ tương ứng giữa đường cao và cạnh đáy bằng nhau hoặc chúng có tỉ lệ nhất định về diện tích với tam giác ABC.

a) Nối A với P, diện tích tam giác ABP và APC bằng nhau vì cạnh đáy PB = PC, chúng có chung đường cao hạ từ đỉnh A xuống cạnh đáy BC, vậy diện tích mỗi tam giác đó bằng .

Tương tự, diện tích tam giác PCM bằng diện tích tam giác PMA vì đáy CM = đáy MA và chúng có chung chiều cao hạ từ đỉnh P xuống đáy AC. Vậy diện tích tam giác PCM bằng:

Tương tự, diện tích tam giác PBN cũng bằng .

Nối BM, và chứng minh tương tự, ta cũng có diện tích tam giác AMN cũng bằng . Từ đó, diện tích MNP cũng bằng .

Vậy

b) Nối CN, ta có diện tích tam giác BMC bằng:

Hai tam giác BMC và BNC có chung đát BC nên chiều cao tương ứng hạ từ M và N xuống đáy BC cũng bằng nhau, nên suy ra MN song song với BC.

Mặt khác, diện tích tam giác MNB bằng . Hai tam giác MNB và BMP có chiều cao hạ từ B xuống MN và từ M xuống BC là chiều cao của hình thang MNBC nên đáy BC gấp 2 lần đáy MN.

Bài 8: Nối AN, diện tích tam giác ABN bằng diện tích tam giác ABC vì đáy BN bằng đáy BC, và chúng có chung chiều cao hạ từ đỉnh A xuống đáy BC.

Diện tích tam giác ABN bằng:

Vì NI song song với AB nên tứ giác NIAB là hình thang. Từ đó, diện tích tam giác IAB bằng diện tích tam giác NAB. Vậy diện tích tam giác IAB cũng bằng

Tương tự, diện tích tam giác IAC cũng bằng diện tích tam giác IBC và bằng .

Bài 9: Ta có:

a)

Vì AC = AB nên suy ra BH = CI

b)

Cộng (1) và (2) ta có:

Vì AB = AC nên:

Suy ra: MQ + MK = BH = 25cm.

Bài 10: C. 36 hình tam giác

Bài 11: A. Diện tích hình tam giác ABM bằng một nưa diện tích ABC

Bài 12:

a) D. 15 đoạn thẳng

b) D. 10 đoạn thẳng

Bài 13: B. 35 hình tam giác

Bài 14: D. 15 hình tam giác

Bài 15: D.

Bài 16: Đáp số: