Trang chủ
LỚP 5 Toán nâng cao Các chuyên đề nâng cao Chuyên đề 3: Hình học Bài 1: Hình tam giác. Diện tích hình tam giác
Bài 1: Hình tam giác. Diện tích hình tam giác
Nội dung chính
- KIẾN THỨC CẦN NHỚ
- 1. Hình tam giác là hình có ba cạnh, ba đỉnh. Đỉnh là điểm hai cạnh tiếp giáp nhau. Cả ba cạnh đều có thể chọn làm đáy của hình tam giác đó.
- 2. Đường cao của tam giác là đoạn thẳng hạ từ đỉnh xuống đáy và vuông góc với đáy. Như vậy, mỗi tam giác sẽ có 3 đường cao.
- 3. Khi vẽ chính xác ba đường cao thì bao giờ chúng cũng gặp nhau tại một điểm (điểm H), điểm đó được gọi là trực tâm của tam giác (Bạn đọc sẽ gặp lại khái niệm này trong chương trình Toán trung học cơ sở)
- 4. Tam giác có ba góc đều nhọn thì cả ba đường cao đều năm trong tam giác.
- 5. Tam giác có góc vuông thì hai cạnh bên của góc vuông chính là chiều cao của tam giác. Chiều cao thứ ba hạ từ đỉnh góc vuông xuống cạnh tương ứng. Chiều cao này nằm trong tam giác (hình 2).
- 6. Tam giác có góc tù thì một đường cao nằm trong tam giác, hai đường cao còn lại nằm ở bên ngoài tam giác (hình 3).
- 7. Các dạng tam giác: Các dạng tam giác này sẽ được nghiên cứu kĩ trong chương trình Toán trung học cơ sở.
- 8. Trong tam giác cân, hai đường cao hạ xuống hai cạnh bằng nhau thì bằng nhau.
- 9. Trong tam giác đều thì ba đường cao đều bằng nhau
- 10. Một số công thức thường vận dụng trong tam giác: Gọi S là diện tích tam giác, a là số đo một cạnh, h là số đo đường cao ứng với cạnh đó (a và h cùng đơn vị đo):
- 11. Hai tam giác có diện tích bằng nhau khi chúng có đáy bằng nhau (hoặc chung đáy) và đường cao bằng nhau (hoặc chung đường cao).
- 12. Hai tam giác có diện tích bằng nhau, đáy bằng nhau thì hai đường cao của hai tam giác ứng với hai cạnh bằng nhau đó cũng bằng nhau.
- 13. Hai tam giác có diện tích bằng nhau, đường cao bằng nhau thì hai đáy của hai tam giác đó ứng với hai đường cao bằng nhau cũng bằng nhau.
- 14. Nếu đáy của tam giác này gấp đáy của tam giác kia bao nhiêu lần và đường cao của tam giác kia cũng gấp đường cao của tam giác bấy nhiêu lần thì hai tam giác đó có diện tích bằng nhau. Nói cách khác:
- 15. Hai tam giác có diện tích bằng nhau có một phần diện tích chung thì phần diện tích còn lại của chúng cũng bằng nhau.
KIẾN THỨC CẦN NHỚ
1. Hình tam giác là hình có ba cạnh, ba đỉnh. Đỉnh là điểm hai cạnh tiếp giáp nhau. Cả ba cạnh đều có thể chọn làm đáy của hình tam giác đó.
2. Đường cao của tam giác là đoạn thẳng hạ từ đỉnh xuống đáy và vuông góc với đáy. Như vậy, mỗi tam giác sẽ có 3 đường cao.
Chẳng hạn,ở hình 1, đường cao hạ từ đỉnh A xuống đáy BC là đoạn AE, trong đó điểm E thuộc đoạn thẳng BC và (đọc là AE vuông góc với BC).
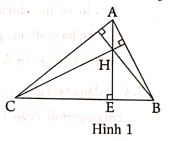
3. Khi vẽ chính xác ba đường cao thì bao giờ chúng cũng gặp nhau tại một điểm (điểm H), điểm đó được gọi là trực tâm của tam giác (Bạn đọc sẽ gặp lại khái niệm này trong chương trình Toán trung học cơ sở)
4. Tam giác có ba góc đều nhọn thì cả ba đường cao đều năm trong tam giác.
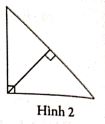
5. Tam giác có góc vuông thì hai cạnh bên của góc vuông chính là chiều cao của tam giác. Chiều cao thứ ba hạ từ đỉnh góc vuông xuống cạnh tương ứng. Chiều cao này nằm trong tam giác (hình 2).
Như vậy, ba đường cao của tam giác vuông gặp nhau tại đỉnh góc vuông.
6. Tam giác có góc tù thì một đường cao nằm trong tam giác, hai đường cao còn lại nằm ở bên ngoài tam giác (hình 3).
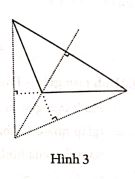
Như vậy, khi vẽ ba đường cao của tam giác chỉ cần vẽ chính xác hai đường cao, đường cao thứ ba sẽ đi qua giao điểm của hai đường cao mà không cần đo góc vuông nữa.
7. Các dạng tam giác: Các dạng tam giác này sẽ được nghiên cứu kĩ trong chương trình Toán trung học cơ sở.
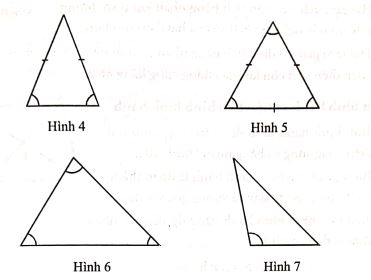
- Tam giác cân: Là tam giác có số đo hai cạnh bằng nhau và khác với số đo cạnh thứ ba (hình 4)
- Tam giác đều: Là tam giác có số đo ba cạnh bằng nhau (hình 5)
- Tam giác vuông cân là tam giác có một góc vuông, hai cạnh kề với góc vuông có số đo bằng nhau
- Tam giác có ba góc nhọn: Là tam giác có cả ba góc nhọn (hình 6)
- Tam giác tù: Là tam giác có một góc tù (hình 7)
8. Trong tam giác cân, hai đường cao hạ xuống hai cạnh bằng nhau thì bằng nhau.
9. Trong tam giác đều thì ba đường cao đều bằng nhau
10. Một số công thức thường vận dụng trong tam giác: Gọi S là diện tích tam giác, a là số đo một cạnh, h là số đo đường cao ứng với cạnh đó (a và h cùng đơn vị đo):
+ S = a x h : 2
+ h = S x 2 : a
+ a = S x 2 : h
11. Hai tam giác có diện tích bằng nhau khi chúng có đáy bằng nhau (hoặc chung đáy) và đường cao bằng nhau (hoặc chung đường cao).
12. Hai tam giác có diện tích bằng nhau, đáy bằng nhau thì hai đường cao của hai tam giác ứng với hai cạnh bằng nhau đó cũng bằng nhau.
13. Hai tam giác có diện tích bằng nhau, đường cao bằng nhau thì hai đáy của hai tam giác đó ứng với hai đường cao bằng nhau cũng bằng nhau.
14. Nếu đáy của tam giác này gấp đáy của tam giác kia bao nhiêu lần và đường cao của tam giác kia cũng gấp đường cao của tam giác bấy nhiêu lần thì hai tam giác đó có diện tích bằng nhau. Nói cách khác:
Hai tam giác có diện tích bằng nhau khi tỉ số đường cao của hai tam giác đó tỉ lệ nghịch với tỉ số của hai đáy của chúng.

