Bài 5: Góc và đường thẳng

1. Góc nhọn, góc tù, góc bẹt

– Khi một góc nhọn không xác định được bằng mắt thì phải dùng ê ke để xác định.

– Khi góc tù không xác định được bằng mắt thì phải dùng ê ke để xác định.

– Muốn xác định một góc bẹt ta có thể dùng thước kẻ để xác định. Đặt thước kẻ trùng sát với một cạnh của góc, nếu cạnh thứ hai cũng trùng sát với cạnh thước kẻ thì góc đó là góc bẹt (cạnh thước phải thật thẳng).

2. Hai đường thẳng song song, cách vẽ.

Muốn vẽ hai đường thẳng song song ta làm như nhau:

Bước 1: Vẽ một đường thẳng.

Bước 2: Vẽ một góc vuông với đường thẳng vừa vẽ.

Bước 3: Vẽ một góc vuông có một cạnh là cạnh góc vuông vừa vẽ.

Ví dụ 1:

 

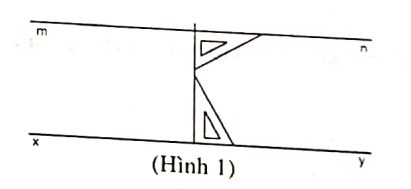
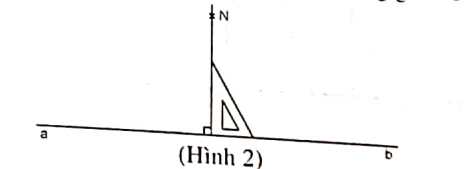
Ví dụ 2: Cho đường thẳng a, b và điểm N nằm ngoài đường thẳng a, b đã cho. Hãy vẽ đường thẳng x, y đi qua điểm N và song song với đường thẳng a, b đã cho.

Giải:

Bước 1. Vẽ đường thẳng đi qua điểm N và vuông góc với đường thẳng a, b đã cho.

Bước 2: Vẽ góc vuông có đỉnh N và một cạnh góc vuông trùng sát với đoạn thẳng qua điểm N vừa vẽ.

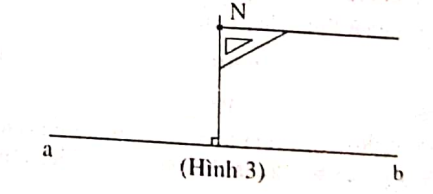
Bước 3: Kéo dài cạnh góc vuông vừa vẽ ta được đường thẳng x, y song song với đường thẳng a, b.

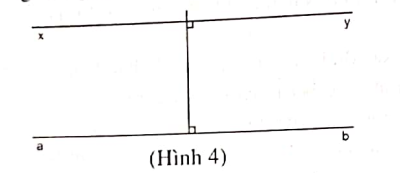
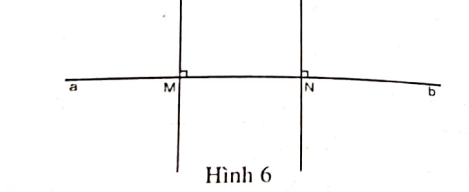
Ví dụ 3: Cho đường thẳng a, b. Hai điểm M, N trên a, b. Hãy vẽ hai đường thẳng đi qua M và N sao cho chúng song song với nhau.

Bước 1: Vẽ hai đường thẳng đi qua M và N và chúng cùng vuông góc với đường thẳng a, b.

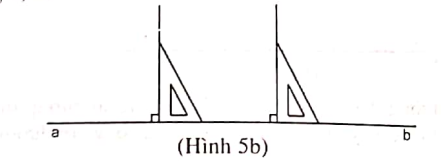
Bước 2: Kéo dài hai đoạn thẳng vừa vẽ vế cả hai đầu, ta được hai đường thẳng cần vẽ.

Chú ý: Khi vẽ hình vuông, hình chữ nhật thì các cặp cạnh đối nhau (hai chiều dài, hai chiều rộng) nhất thiết phải song song với nhau.

3. Ôn tập và mở rộng thêm về hình chữ nhật, hình vuông.

3.1.

a) Muốn tính diện tích hình chữ nhật ta lấy số đo chiều dài nhân với số đo chiều rộng (cùng đơn vị đo)

(a là chiều dài, b là chiều rộng)

b) Muốn tính diện tích hình vuông ta lấy số đo cạnh nhân với chính nó.

(a là số đo cạnh hình vuông)

c) Muốn tính chiều dài hình chữ nhật ta lấy số đo diện tích chia cho số đo chiều rộng.

(Trong đó a là chiều dài, S là diện tích, b là chiều rộng)

d) Muốn tính chiều rộng hình chữ nhật ta lấy số đo diện tích chia cho số đo chiều dài.

3.2. Hai hình chữ nhật A và B có diện tích bằng nhau, nếu chiều rộng của hai hình chữ nhật bằng nhau thì chiều dài của hai hình cũng bằng nhau và ngược lại.

3.3. Hai hình chữ nhật A và B có diện tích bằng nhau, nếu chiều rộng của hình A gấp chiều rộng của hình B bao nhiêu lần thì chiều dài của hình B cũng gấp chiều dài của hình A bấy nhiêu lần.

3.4. Hai hình chữ nhật (hoặc hình vuông) A và B có diện tích bằng nhau và chúng có một phần diện tích chung nhau thì diện tích phần còn lại của chúng cũng bằng nhau.

3.5. Hai hình chữ nhật A và B có chiều rộng (hoặc chiều dài) bằng nhau, nếu diện tích hình A gấp diện tích hình B bao nhiêu lần thì chiều dài (hoặc chiều rộng) hình A cũng gấp chiều dài (hoặc chiều rộng) hình B bấy nhiêu lần.

3.6. Hai hình vuông có số đo cạnh (kích thước) gấp nhau bao nhiêu lần thì diện tích của chúng gấp nhau một số lần bằng một số lần gấp của kích thước nhân với chính nó.

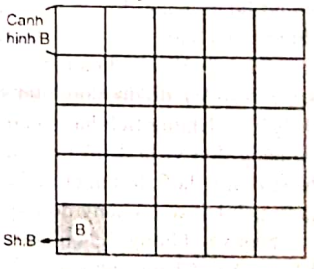
Chẳng hạn: Hai hình vuông có số đo cạnh gấp nhau 5 lần thì diện tích của chúng gấp nhau số lần là:

5 x 5 = 25 (lần)

lần

Một số bài toán:

Bài toán 1: Diện tích một hình chữ nhật là 7209. Chiều dài hình chữ nhật là 89m. Tính chu vi hình chữ nhật đó.

Giải:

Chiều rộng hình chữ nhật là:

7209 : 89 = 81 (m)

Nửa chu vi hình chữ nhật là:

89 + 81 = 170 (m)

Chu vi hình chữ nhật là:

170 x 2 = 340 (m)

Đáp số: 340m

 

Bài toán 2: Một hình chữ nhật có chu vi là 198m. Chiều dài hơn chiều rộng 17m. Tính diện tích hình chữ nhật đó.

Giải:

Nửa chu vi hình chữ nhật là:

198 : 2 = 99 (m)

Chiều rộng hình chữ nhật là:

(99 – 17) : 2 = 41 (m)

Chiều dài hình chữ nhật là:

41 + 17 = 58 (m)

Diện tích hình chữ nhật là:

58 x 41 = 2378 ()

Đáp số: 2378

 

Bài toán 3. Bạn Châm tính diện tích một hình vuông và tìm được kết quả là 277. Hỏi bạn Châm tính đúng hay sai ? Vì sao ?

Giải

Cách 1. Bạn Châm tính sai vì không có số tự nhiên nhân với chính số đó lại có hàng đơn vị là 7. Cụ thể, một số tự nhiên nhân với chính nó thì được số có hàng đơn vị là: 0, 1, 4, 5, 6, 9.

Cách 2. Vì 277 là số lẻ nên số đo cạnh hình vuông là số lẻ (tích của hai số lẻ là số lẻ), do đó hàng đơn vị của số đo cạnh hình vuông chỉ có thể là: 1, 3, 5, 7, 9. Nhưng tích hai số có hàng đơn vị là 1 thì tận cùng là 1; tích hai số có hàng đơn vị là 3 thì tận cùng (hoặc có hàng đơn vị) là 9; tích hai số có hàng đơn vị là 5 thì tận cùng là 5; tích hai số có hàng đơn vị là 7 thì tận cùng là 9; tích hai số có hàng đơn vị là 9 thì tận cùng là 1.

Như vậy không thể có hình vuông có số đo diện tích hàng đơn vị là 7. Vì vậy, bạn Châm tính sai.

 

Bài toán 4. Hai hình vuông có tổng chu vi là 136cm. Hiệu số đo hai cạnh hình vuông là 4cm. Tính diện tích mỗi hình vuông.

Phân tích: Hình vuông là hình có 4 cạnh bằng nhau (và có 4 góc vuông), như vậy:

136 = cạnh hình vuông lớn x 4 + cạnh hình vuông bé x 4

= (cạnh hình vuông lớn + cạnh hình vuông bé) x 4

Giải

Tổng số đo cạnh của hai hình vuông là:

136 : 4 = 34 (cm)

Cạnh hình vuông lớn là:

(34 + 4) : 2 = 19 (cm)

Cạnh hình vuông bé là:

19 – 4 = 15 (cm)

Diện tích hình vuông lớn là:

19 x 19 = 361 ()

Diện tích hình vuông bé là:

15 x 15 = 225 ()

Đáp số: 361 và 225

 

Bài toán 5. Hai cái đáy thùng hình vuông có kích thước gấp nhau 4 lần và cũng được cắt ra từ một lá tôn. Tổng khối lượng của hai đáy thùng là 3400g. Tính khối lượng mỗi đáy thùng.

Giải

Hai đáy thùng hình vuông gấp nhau 4 lần thì diện tích của chúng gấp nhau số lần là:

4 x 4 = 16 (lần)

Chúng lại được cắt ra từ một lá tôn nên khối lượng chúng cũng gấp nhau 16 lần.

Ta có sơ đồ sau:

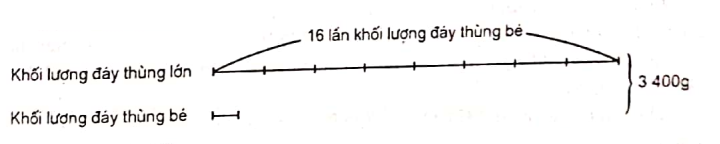
3400g bằng mấy lần khối lượng đáy thùng bé ?

16 + 1 = 17 (lần)

Khối lượng đáy thùng bé là:

3400 : 17 = 200 (g)

Khối lượng đáy thùng lớn là:

3400 – 200 = 3200 (g)

Đáp số: 200g;  3200g

 

Bài toán 6: Trên một nửa thửa đất hình vuông người ta đào một cái áo hình vuông, cạnh ao song song với cạnh thửa đất và cách đều cạnh thửa đất. Chu vi thửa đất hơn chu vi ao là 40m. Diện tích đất còn lại là 420. Tính diện tích ao.

Phân tích: Hình vuông có 4 cạnh bằng nhau nên một cạnh thửa đất hơn một cạnh ao là: 40 : 4 = 10 (m). Do đó, cạnh ao cách cạnh thửa đất là 5m. Ta chia chỗ đất còn lại thành 4 hình chữ nhật: 1, 2, 3, 4 có diện tích bằng nhau vì chiều rộng mỗi hình đều là: 10 : 2 = 5 (m), chiều dài mỗi hình đều bằng cạnh ao cộng 5m (hoặc cạnh thửa đất trừ 5m). Từ đó, tính được diện tích mỗi hình chữ nhật; chiều dài hình chữ nhật; cạnh ao; diện tích ao.

Giải

Cạnh thửa đất hơn cạnh ao là:

40 : 4 = 10 (m)

Chiều rộng mỗi hình chữ nhật là:

10 : 2 = 5 (m)

Diện tích mỗi hình chữ nhật là:

420 : 4 = 105 ()

Chiều dài mỗi hình chữ nhật là:

105 : 5 = 21 (m)

Cạnh ao là:

21 – 5 = 16 (m)

Diện tích ao là:

16 x 16 = 256 ()

Đáp số: 256

 

Bài toán 7. Một thửa đất hình chữ nhật có chu vi là 106m. Nếu giảm chiều dài 5m, tăng chiều rộng 5m thì diện tích của hình không thay đổi. Tính diện tích thửa đất đó.

Phân tích: Vì diện tích của hình không thay đổi nên diện tích hình chữ nhật ABCD bằng diện tích hình chữ nhật AMNP. Chúng lại có phần diện tích chung là tứ giác AMQD nên diện tích hình chữ nhật MBCQ bằng diện tích hình chữ nhật DQNP.

Hai hình chữ nhật MBCQ và DQNP cùng có chiều rộng là 5m nên chiều dài của chúng phải bằng nhau tức là MQ bằng QD.

Từ đó, chiều dài AB hơn chiều rộng AD là 5m.

Giải tiếp: Vì diện tích hình chữ nhật là không đổi nên:

Chúng lại có các chiều rộng MB bằng QN bằng 5m nên chiều dài MQ bằng chiều dài QD. Do vậy, chiều dài AB hơn chiều rộng AD là 5m.

Nửa chu vi hình chữ nhật ABCD là:

106 : 2 = 53 (m)

Chiều rộng hình chữ nhật là:

(53 – 5) : 2 = 24 (m)

Chiều dài hình chữ nhật là:

24 + 5 = 29 (m)

Diện tích hình chữ nhật là:

24 x 29 = 696 ()

Đáp số: 696

Xem thêm: Bài 6: Dãy số