Bài 8: Ôn tập tìm hai số khi biết tổng hoặc hiệu và tỉ số của chúng (tiếp)
Nội dung chính
PHẦN I. ĐỀ BÀI
Bài 1:
Cho 20 số tự nhiên liên tiếp bắt đầu từ 2. Hãy tìm xem trong 20 số đó những số nào chỉ chia hết cho 1 và chính nó.
Bài 2:
Cho 3 số cách đều nhau: . Hãy tìm 3 số đó.
Bài 3:
a) Tại sao khi cộng các số tự nhiên nếu tổng các chữ số ở mỗi cột (kể cả số nhớ sang) nếu quá 9; 19; 29,… thì ta nhớ 1; 2; 3 sang cột liền bên trái?
b) Ở phép cộng số đo thời gian khi tổng số giây, phút, giờ (kể cả số nhớ sang) quá bao nhiêu thì nhớ 1 đơn vị sang hàng đơn vị kề bên trái? Tại sao?
Bài 4:
a) Khi cộng môt dãy số cách đều nhau, nếu số các số hạng là số chẵn ta sắp các cặp số từ hai đầu dãy số vào và được các cặp số đều có tổng bằng nhau rồi lấy tổng của một cặp số nhân với số cặp số thì đươc tổng của dãy số.
Em hãy giải thích khi làm từng bước các việc trên ta đã dựa vào những tính chất nào của phép cộng?
b) Khi số các số hạng là số lẻ thì làm thế nào để tính tổng đó được nhanh?
Bài 5:
Muốn tính trung bình cộng của các số cách đều nhau ta làm thế nào cho nhanh?
Bài 6:
a) Hiệu của hai số tư nhiên liên tiếp là chữ số nào? Tại sao?
b) Hiệu của hai số chẵn liên tiếp là chữ số nào? Tại sao?
c) Hiệu của hai số lẻ liên tiếp là chữ số nào? Tại sao?
Bài 7:
Khi nào thì hiệu của hai số chia hết cho 7?
Bài 8:
Khi chọn một số có một chữ số, đem số đã chọn nhân với 9 được bao nhiêu đem nhân với số 12345679 thì được tính là số gồm toàn các chữ số đã chọn.
Em hãy giải thích điều đó và nói rõ em đã dùng tính chất nào của phép nhân?
Bài 9:
Khi chọn một số có hai chữ số mà tổng của hai chữ số của só đó nhỏ hơn 10, đem số đã chọn nhân với 9, đem tích vừa nhân nhân với số 12345679 thì được tích là một số như thế nào? (Nêu rõ đặc điểm của tích cuối cùng)
Bài 10:
Hoà khoe với An là tìm được hai số tự nhiên liên tiếp có tích là 13579. Điều Hoà nói có đúng không? Tại sao?
Bài 11:
Tích của hai số tự nhiên bằng nhau có thể có hàng đơn vị là 2 không?
Bài 12:
Khi nào thì tích của hai số tự nhiên có hàng đơn vị là 0?
Bài 13:
Một số lẻ không chia hết cho số chẵn. Tại sao?
Bài 14:
Cho hai số 53 và 75. Hãy tìm một số sao cho khi cộng số đó với một số trong hai số đã cho và đem số còn lại trong hai số đã cho trừ đi số đó thì được hai số mới và thương giữa hai số mới bằng:
a) 7
b) 1
c) 3
d) 0
Bài 15:
Tìm số nhỏ nhất có 4 chữ số sao cho khi đem số đó chia cho 175 thì được số dư là số dư lớn nhất.
Bài 16:
Tìm số chẵn nhỏ nhất sao cho khi đem số đó chia cho 765 thì được số dư lớn nhất.
Bài 17:
Cho số A. Biết số A chia cho 499 thì được thương là số có hai chữ số và dư 357. Hỏi:
a) Phải bớt ở số A bao nhiêu đơn vị để phép chia là phép chia hết và thương giảm 2 đơn vị?
b) Phải thêm vào số A bao nhiêu đơn vị để phép chia là phép chia hết và thương tăng 3 đơn vị.
Bài 18:
Một hình chữ nhật có số đo chiều dài, chiều rộng là số tự nhiên. Người ta chia hình chữ nhật đó thành hai hình chữ nhật nhỏ. Có thể có tổng chu vi của hai hình chữ nhật nhỏ là số lớn nhất có 3 chữ số không?
Bài 19:
Tìm số có 3 chữ số có tổng các chữ số là 20 và tỉ số giữa chữ số hàng trăm với chữ số hàng đơn vị là 2, còn chữ số hàng chục bằng chữ số hàng trăm.
Bài 20:
Cho số có hai chữ số có tổng của số đó với các chữ số của nó là 15 và tỉ số của số đó với tổng các chữ số của nó là 4. Tìm số đã cho.
Bài 21:
Cho một số mà chia cho 11 hoặc 14 đều dư 9. Thương của số đó khi chia cho 11 lớn hơn thương của só đó khi chia cho 14 là 3. Tìm số đó.
Bài 22:
Đi đoạn đường AB với vận tốc 35km một giờ thì phải đi hết 8 giờ. Hỏi đi đoạn đường AB với vận tốc 40km một giờ thi phải đi hết mấy giờ?
Bài 23:
Toán vui (phỏng theo một bài toán cổ)
Trong buổi liên hoan lớp, sau khi đã tàn bữa, Hoàn bảo Toàn: “Vừa qua bạn đạt giải nhì kì thi học sinh giỏi khu vực Đông Nam Á. Mình xin phép thay mặt lớp chúc mừng cậu. Có hai cách chúc mừng: Một là 1 cái bánh ga tô. Hai là 1 cốc nước ngọt nhưng cậu phải ăn hoặc uông ở đây, không được mang về. Nếu cậu đoán đúng cậu phải nhận thứ gì thì cậu được cái bánh. Nếu đoán sai thì uống cốc nước ngọt.”
Cả lớp đều hoan hô Hoàn, Toàn suy nghĩ rồi nói: ” Để cho nhanh tớ đoán: Cậu định cho mình uống nước ngọt”. Mọi người lại hoan hô, riêng Hoàn đứng ngẩn người ra. (Vì Hoàn cũng rất giỏi toán). Hỏi Toàn sẽ phải nhận thứ gì?
Bánh hay nước ngọt?
PHẦN II. LỜI GIẢI
Bài 1:
20 số tự nhiên liên tiếp bắt đầu từ 2 là: 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21.
Trong đó các số chia hết cho 2 là (không kể số 3 vì số 3 là chính số đó): 6; 9; 12; 15; 18; 21.
Các số chia hết cho 5: 10; 15; 20.
Không kể các số chia hêt cho 6 vì 6 chia hết cho 2 và 3.
Các số chia hết cho 7: 14 và 21.
Không xét các số 8; 9; 20 vì 8 chia hết cho 2; 9 chia hết cho 3 và 10 chia hết cho 2; 5.
…
Vậy 20 số tự nhiên liên tiếp bắt đầu từ 2 thì các số chỉ chia hết cho 1 và chình nó là: 2; 3; 5; 7; 11; 13; 17; 19
Bài 2:
Ba số cách đều nhau nên:
Vậy a = 1
Vì có hàng đơn vị là 0 và
Thay a = 1 ta có:
Từ đó:
Đáp số: 16; 61; 106
Bài 3:
a) Số tự nhiên thuộc hệ thập phân, hai đơn vị kế tiếp nhau gấp nhau 10 lần
b) Quá 59 giây nhớ 1 sang hàng phút, quá 59 phút nhớ 1 sang hàng giờ vì 1 giờ có 60 phút, 1 phút có 60 giây. Quá 23 giờ nhớ 1 sang hàng ngày vì 1 ngày có 24 giờ.
Bài 4:
a) Thí dụ: 12; 15; 18; 21; 24; 27 thì:
12 + 27 = 15 = 24 = 18 + 21 Vì 15 hơn 12 là 3 thì 24 kém 27 là 3; 18 hơn 15 là 3 thì 21 kém 24 là 3
Khi thêm vào số hạng này bao nhiêu đơn vị và bớt ở số hạng kia bấy nhiêu đơn vị thì tổng hai số vẫn không đổi. Vì vậy, tổng các cặp số đều bằng nhau. Mặt khác, số lượng số hạng là số chẵn nên khi sắp các cặp số sẽ vừa đủ cặp.
b) Khi số các số hạng là lẻ, ta để lại số hạng đầu (hoặc cuối) để còn lại một số chẵn số hạng đủ sắp xếp các cặp số có tổng bằng nhau, lấy tổng của một cặp nhân với số cặp rồi cộng với số hạng còn lại.
Thí du: 1 + 3 + 5 + 7 + 9, ta có: 3 + 9 = 12; 5 + 7 = 12
12 x 2 + 1 = 25
Nếu biết số hạng ở chính giữa dãy số, ta lấy số hạng đó nhân với số lượng số hạng
Thí dụ: Số hạng ở chính giữa dãy số trên là 5, dãy số có 5 số hạng nên tổng của dãy số bằng: 5 x 5 = 25
Bài 5:
1) Lấy tổng của dãy số chia cho số lượng số hạng.
2) Nếu dãy số có số lượng số hạng là số chẵn thì trung bình cộng của dãy số bằng tổng của một cặp số sắp xếp từ hai đầu dãy số vào chia cho 2.
3) Nếu dãy số có số lượng số hạng là số lẻ, ta lấy tổng của một cặp số sắp xếp từ hai đầu dãy số vào chia cho 2 hoặc trung bình cộng của dãy số bằng số hạng ở chính giữa dãy số.
Bài 6:
a) Hai số tự nhiên liên tiếp hơn (kém) nhau 1 đơn vị. Vậy hiệu của chúng bằng 1.
b) Hai số chẵn liên tiếp hơn (kém) nhau 2 đơn vị. Vậy hiệu của chúng là 2.
c) Hai số lẻ liên tiếp hơn (kém) nhau 2 đơn vị. Vậy hiệu của chúng bằng 2.
Bài 7:
Hiệu của hai số chia hết cho 7 khi:
- Cả hai số đó chia hết cho 7
Thí dụ: 70 và 91 cùng chia hết cho 7 và 91 – 70 = 21 chia hết cho 7.
- Cả hai số đó chia cho 7 có cùng một số dư
Thí dụ: 99 và 113 chia cho 7 đều dư 1, 113 – 99 = 14 chia hết cho 7
Bài 8:
Giả sử ta chọn số 7. Theo đề bài ta có:
7 x 9 x 12345679 = 7 x (9 x 12345679) = 7 x 111111111
Vậy tích sẽ là số gồm 9 chữ số 7 đã chọn.
Bài 9:
Giả sử ta chọn số 36. Theo đề bài ta có:
36 x 9 x 12345679 = 36 x (9 x 12345679) = 36 x 111111111
Tích riêng thứ nhất là số gồm 9 chữ số 6.
Tích riêng thứ hai là số gồm 9 chữ số 3.
Tích chung có hàng đơn vị là 6, chữ số hàng nghìn triệu là 3. Các chữ số còn lại ở giữa là 9 vì 6 + 3 = 9 không có nhớ,
Bài 10:
Hoà nói sai. Hai số tự nhiên liên tiếp gồm một số lẻ và một số chẵn. Tích của số chẵn với số bất kì là số chẵn. Còn số 13579 là số lẻ nên sai.
Bài 11:
Tích hai số tự nhiên bằng nhau không thể có hàng đơn vị là 2 vì đó phải là tích của hai số chẵn. Nên có hàng đơn vị là 0; 2; 4; 6; 8
Mà 0 x 0 = 0; 2 x 2 = 4; 6 x 6 = 36; 8 x 8 = 64
Bài 12:
Có hai trường hợp tích của hai số tự nhiên có hàng đơn vị là 0 là
- Trong 2 số tự nhiên có ít nhất một số có hàng đơn vị là 0.
- Trong 2 số tự nhiên có một số là số chẵn, số còn lại có hàng đơn vị là 5.
Chẳng hạn:
2 x 5 = 10; 4 x 5 = 20; 6 x 5 = 30; 8 x 5 = 40.
Bài 13:
Một số lẻ không thể chia hết cho số chẵn. Thật vậy, giả sử có một số lẻ nào đó chia hết cho số chẵn thì ta có:
Số lẻ: số chẵn = A (A là số tự nhiên)
Số lẻ = số chẵn x A
Số lẻ = số chẵn
Điều đó vô lý và chứng tỏ số lẻ không chia hết cho số chẵn.
Bài 14:
Tổng của hai số đó là:
53 + 75 = 128
Khi thêm vào một trong hai số đã cho bao nhiêu đơn vị và bớt ở số hạng kia bấy nhiêu đơn vị thì tổng của hai số không thay đổi và bằng 128
a) Thương giữa hai số bằng 7 thì số lớn bằng 7 lần số bé.
Số bé mới là:
128 : (7 + 1) = 16
Số lớn mới là:
128 – 16 = 112
Nếu số lớn bị bớt thì số cần tìm là:
75 – 16 = 59 = 112 – 53
Nếu số bé bị bớt thì số cần tìm là:
53 – 16 = 37
b) Hai số mới đều bằng nhau và là:
128 : 2 = 64
Vì 64 > 53 nên chỉ có thể bớt ở số 75 và số cần tìm là:
75 – 64 = 11
c) Số bé mới là:
128 : (3 + 1) = 32
Số cần tìm là:
75 – 32 = 43
d) Thương bằng 0 khi một trong hai số là 0, số kia là 128 vì 0 chia hết cho bất cứ số nào lớn hơn 0 cũng cho thương là 0. Khi đó số cần tìm là 75 hoặc 53
Đáp số:
a) 59 hoặc 37
b) 11
c) 43 hoặc 21
d) 75 hoặc 53
Bài 15:
Ta thấy 1000 : 75 = 5 dư 125 (1000 là số nhỏ nhất có 4 chữ số)
Số dư lớn nhất kém số chia 1 đơn vị nên là:
175 – 1 = 174
Phải thêm vào 1000 bao nhiêu đơn vị để được số dư lớn nhất?
174 – 125 = 49
Số phải tìm là:
1000 + 49 = 1049
Đáp số: 1049
Bài 16:
Số dư lớn nhất là:
765 – 1 = 764
Vì số chia là số chẵn, số dư là số chẵn nên số chia nhân với số thương phải có tích là số chẵn để số chẵn cộng với số chẵn bằng số chẵn, Số chia là 765 là số lẻ nên thương số phải là số chẵn. Để số bị chia là nhỏ nhất thì thương phải nhỏ nhất nên phải là 0. Vậy số cần tìm là:
765 x 0 + 764 = 764
Đáp số: 764
Bài 17:
Phải bớt ở số A là:
479 x 2 + 357 = 1315
b) Phải thêm vào số A là:
479 x 3 – 357 = 1020
Bài 18:
Có hai cách chia một hình chữ nhật thành hai hình chữ nhật nhỏ như hình 24 dưới đây:
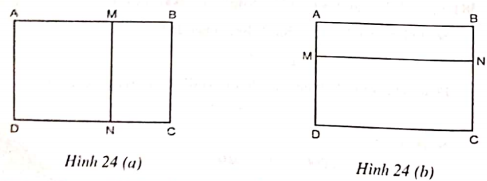

Quan sát hình a và b ta thấy tổng chu vi của hai hình chữ nhật nhỏ bằng chu vi hình chữ nhật đã cho cộng hai lần MN nên:
(d + r) x 2 + MN x 2 = (d + r + MN) x 2 = số chẵn
Còn số lớn nhất có ba chữ số là 999 là số lẻ. Vậy tổng chu vi hai hình chữ nhật nhỏ hơn không thể bằng 999.
Đáp số: Không thể
Bài 19:
Theo đề bài ta có:
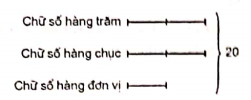

Số hàng đơn vị là:
20 : (2 + 2 + 1) = 4
Chữ số hàng trăm và chục là:
4 x 2 = 8
Số phải tìm là: 884
Đáp số: 884
Bài 20:
Tổng các chữ số đó là:
15 : (4 + 1) = 3
Số đó là:
3 x 4 = 12
Đáp số: 12
Bài 21:
Nếu bớt ở số đó 9 đơn vị ta được số mới chia hết cho 11 và 14. Muốn thương giữa số mới và 11 cũng bằng thương giữa số mới với 14 thì khi chia số mới cho 11 cần bớt ở số mới là:
11 x 3 = 33 (đơn vị)
Hiêu giữa 14 và 11 là:
14 – 11 = 3
Thương giữa số phải tìm với 14 là;
33 : 3 = 11
Số phải tìm là:
14 x 11 + 9 = 163
Đáp số: 163
Bài 22:
Đáp số: 7 giờ
Bài 23:
Hoàn ngẩn người ra vì không có cách xử lý. Ví dụ: Hoàn nói Toàn đúng thì Toàn phải ăn bánh. Khi đó thành ra Toàn sai, mà đoán sai thì phải uống nước ngọt nên lại thành đúng.
Vậy Toàn không phải nhận thứ gì cả. Toàn thoát không phải ăn bánh cũng không phải uống nước ngọt vì bụng đã “no đủ” rồi.
Xem thêm: Toán nâng cao lớp 5 – Chuyên đề 1 – Bài 1 Kiến thức cần lưu ý

